15.1. 指数(exponential)分布
泊松(Poisson)分布是预测在一个固定时间间隔内,随机事件发生n次的概率。
而指数分布是预测下一次时间发生需要等待多长的时间。
比如,下面几种情况:
直到客户下次购买商品为止(成功)的时间。
机器下次发生故障的时间。
下次公交车到达需要等待的时间。
15.1.1. 推导过程
在泊松分布中有一个参数 \(\lambda\) ,其表示在单位时间区间内事件发生次数的平均值,
其是一个单位时间的比例(rate)值。
那么 \(\lambda\) 倒数 \(1/\lambda\) 是什么含义呢?
\(1/\lambda\) 就表示 事件发生一次需要的时间的平均值。
比如,当 \(\lambda=0.25\) 时,表示在单位时间内平均发生了0.25次,
倒过来( \(1/\lambda=1/0.25=4\) )就是发生一次需要4个单位时间。
指数概率分布表示,在一个泊松过程中,两次事件发生的间隔时间的概率分布。
用泊松分布的表达就是在等待的之间范围内一次事件都没发生,这意味着有
\(Poisson(x=0)\) 。
(15.1.1)\[ \begin{align}\begin{aligned}p(x=k) &= \frac{\lambda^k e^{-\lambda}}{k!}\\p(x=0) &= \frac{\lambda^0 e^{-\lambda}}{0!} = e^{-\lambda}\end{aligned}\end{align} \]
需要注意的是,在泊松分布的概率函数中时间间隔仅仅是1个单位时间(unit time)。
如果想要建立一个在任意时间区间t(而不是一个单位时间)无事件发生的概率分布,
我们需要做些什么呢?
泊松分布假设事件之间是相互独立的,计算t个单位时间内0次发生的概率可以是每个单位时间内0次发生概率的连乘。
(15.1.2)\[ \begin{align}\begin{aligned}\underbrace{p(T>t)}_{\text{在t个单位时间内没有发生}}
&= \underbrace{p(x=0 )}_{\text{第1个单位时间}} \times \underbrace{p(x=0)}_{ \text{第2个单位时间}}
... \underbrace{p(x=0 )}_{\text{第t个单位时间}}\\&= e^{-\lambda t}\end{aligned}\end{align} \]
\(T\) 表示下次事件发生的时间,\(p(T>t)\) 就表示下次事件发生的时间晚于t的概率,换句话说,
就是 \(t\) 时间内没有发生的概率。那么 \(t\) 时间内发生的概率就是:
(15.1.3)\[p(T \le t) = 1- p(T>t) = 1 - e^{-\lambda t}\]
上式是累计分布函数(cumulative distribution function,CDF),
通过对CDF进行微分(求导)就得到了分布的概率密度函数(probability distribution function,PDF)。
(15.1.4)\[f(t) = \frac{d p(T \le t)}{d t} = \lambda e^{-\lambda t}\]
如果单位时间内事件发生次数符合泊松分布,那么事件发生的间隔时间就服从指数分布。
15.1.2. 分布的特性
15.1.2.1. 曲线图
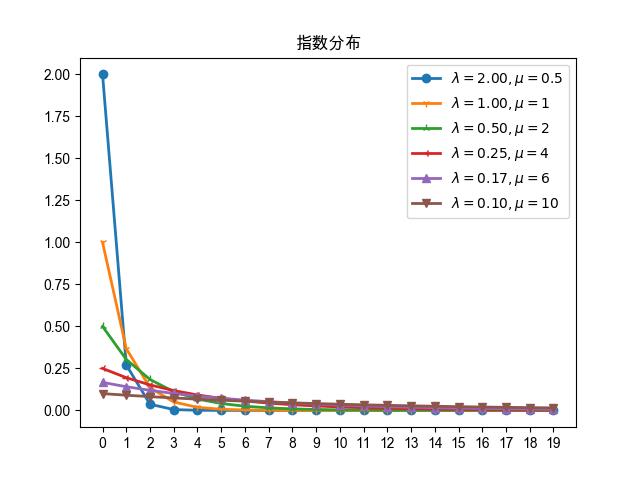
图 15.1.1 指数分布的概率密度函数
15.2. 指数回归模型
指数分布的概率分布函数通常写成如下的形式:
(15.2.1)\[\begin{split}f(y;\lambda)=
\begin{cases}
\lambda e^{-\lambda y} & y \ge 0 \\
0 & y<0
\end{cases}\end{split}\]
其中 \(\lambda >0\) 是分布的一个参数,常被称为率参数(rate parameter),
即每单位时间发生该事件的次数。指数分布的区间是 \([0,\infty)\)
只有 \(y \ge 0\) 才有意义。
如果一个随机变量 \(Y\) 呈指数分布,则可以写作:\(Y \sim Exponential(\lambda)\)
。
指数分布的响应变量的值是大于等于0的,从概率密度函数的图形上可以看出,0的概率是最大的,
并且值越大概率越小,是一个递减的非对称结构,这和高斯模型的对称结构是完全一样的。
指数分布的期望为:
(15.2.2)\[\mathbb{E}[Y] = \frac{1}{\lambda} = \mu\]
方差为:
(15.2.3)\[Var(Y) = \frac{1}{\lambda^2}\]
指数分布的期望 \(\mu\) 和比率参数 \(\lambda\) 互为倒数的关系,二者是一一映射的,
所以可以用 \(\mu\) 参数化概率密度函数。
(15.2.4)\[f(y;\mu) = \frac{1}{\mu} e^{- \frac{y}{\mu}}\]
现在我们把 公式(15.2.4) 转化成GLM的形式。
(15.2.5)\[f(y;\mu)= \exp \{ - \frac{y}{\mu} + \ln \left ( \frac{1}{\mu} \right ) \}\]
GLM中指数族分布标准形式为:
(15.2.6)\[p(y|\theta) = \exp \{\frac{\theta y - b(\theta)}{a(\phi)} + c(y,\phi)\}\]
对比下 公式(15.2.4) 和 公式(15.2.6)
,可以直接给出各个组件的内容。
(15.2.7)\[ \begin{align}\begin{aligned}\theta &= - \frac{1}{\mu}\\b(\theta) &= - \ln \left ( \frac{1}{\mu} \right )\\a(\phi) &= \phi= 1\end{aligned}\end{align} \]
现在我们来看下 \(b(\theta)\) 的导数。
(15.2.8)\[ \begin{align}\begin{aligned}b'(\theta) &= \frac{\partial b}{\partial \mu} \frac{\partial \mu}{\partial \theta}\\&= \left (-1 \times \mu \frac{-1}{\mu^2} \right )( \mu^2)\\&= \mu\\
b''(\theta) &= \frac{\partial^2 b}{\partial \theta^2}\\&= \frac{\partial }{\partial \theta} \left ( \frac{\partial b}{\partial \mu} \frac{\partial \mu}{\partial \theta} \right )\\&= \frac{\partial }{\partial \theta}(\mu)\\&= \frac{\partial }{\partial \mu} \mu \frac{\partial \mu}{\partial \theta}\\&= (1)(\mu^2)=\mu^2 = \nu(\mu)\end{aligned}\end{align} \]
指数分布的方差函数为 \(\nu(\mu)=\mu^2\)
,分散函数为 \(a(\phi)=1\)
,因此指数分布的方差为:
(15.2.9)\[Var(y) = a(\phi)\nu(\mu) = \mu^2\]
显然指数分布的方差与期望是平方关系,这与高斯分布是不一样的,高斯分布的方差与期望是无关的。
指数分布的 \(a(\phi)=1\) 使其不再需要一个额外的分散参数 \(\phi\)
,只需要一个期望参数即可,这使得指数分布是一个单参数模型。
根据规范连接函数的定义,指数分布的标准连接函数是负倒数函数。
(15.2.10)\[ \begin{align}\begin{aligned}\text{标准连接函数:} &\eta=\theta=g(\mu) = - \frac{1}{\mu}\\\text{标准响应函数:} &\mu = - \frac{1}{\eta}\end{aligned}\end{align} \]
连接函数的导数可以简单得到。
(15.2.11)\[g'(\mu) = \frac{1}{\mu^2}\]
采用标准链接的指数分布模型,通常又被称为指数回归模型(exponential regression),
经常用来处理正数响应数据。
15.3. 参数估计
15.3.1. 似然函数
指数分布的对数似然函数形式比较简单,因为其没有 \(c(y,\phi)\) 这一项。
(15.3.1)\[\ell(\hat{\mu};y) = \sum_{n=1}^{N} \left \{
- \frac{y_i}{\mu_i} + \ln \left ( \frac{1}{\mu_i} \right )
\right \}\]
对数似然函数的一阶导数又叫做得分统计量,或者得分函数(score function),
用符号 \(U\) 表示,
似然估计目标就是求解方程 \(U=0\)
。
(15.3.2)\[ \begin{align}\begin{aligned}U &= \frac{\partial \ell}{\partial \mu_i}\\&=\sum_{i=1}^{N} \left \{
\frac{y_i}{\mu_i^2} - \frac{1}{\mu_i}
\right \}\end{aligned}\end{align} \]
连接函数是标准连接函数的情况下,用 \(\beta\) 重新参数化似然函数。
(15.3.3)\[ \begin{align}\begin{aligned}\ell(\beta;y) &= \sum_{n=1}^{N} \left \{
- \frac{y_i}{\mu_i} + \ln \left ( \frac{1}{\mu_i} \right )
\right \}\\&= \sum_{i=1}^{N} \left \{
\eta_i y_i + \ln \left ( -\eta_i \right ) \right \}\\&= \sum_{i=1}^{N} \left \{
( x_i\beta) y_i + \ln \left ( - x_i\beta \right ) \right \}\end{aligned}\end{align} \]
(15.3.4)\[U_j = \frac{\partial \ell}{\partial \beta_j} =
\sum_{i=1}^{N} y_i x_{ij} + \frac{x_{ij}}{ x_i\beta}
= \sum_{i=1}^{N} \left ( y_i - \frac{1}{ x_i\beta} \right ) x_{ij}\]
\(x_i\) 是行向量,\(\beta\) 是参数列向量,二者內积是一个标量。
15.3.2. 拟合优度
现在我们来看下模型的偏差(Deviance),
首先写出饱和模型的似然函数,
只需要把 公式(15.3.1) 中的 \(\hat{\mu}_i\)
替换成 \(y_i\) 即可。
(15.3.5)\[ \begin{align}\begin{aligned}\ell(y;y) &= \sum_{n=1}^{N} \left \{
- \frac{y_i}{y_i} + \ln \left ( \frac{1}{y_i} \right )
\right \}\\&= \sum_{n=1}^{N} \left \{ -1 - \ln(y_i) \right \}\end{aligned}\end{align} \]
模型的偏差为:
(15.3.6)\[ \begin{align}\begin{aligned}D &= 2 \{ \ell(y;y) - \ell(\hat{\mu};y) \}\\&= 2\sum_{n=1}^{N} \left \{
-1 - \ln(y_i) + \frac{y_i}{\hat{\mu}_i} - \ln \left ( \frac{1}{\hat{\mu}_i} \right )
\right \}\\&= 2\sum_{n=1}^{N} \left \{ \frac{y_i}{\hat{\mu}_i} -\ln \left ( \frac{y_i}{\hat{\mu}_i} \right ) -1
\right \}\end{aligned}\end{align} \]
高斯分布存在分散参数 \(a(\phi)=\sigma^2\) 。
指数分布是没有分散参数 \(\phi\) 的,
因此指数分布模型的偏差和尺度化偏差是一样的。
高斯分布的方差函数是常量 \(\nu(\mu)=1\) ,
然而指数分布的方差函数是 \(\nu(\mu) = \mu^2\) ,
指数分布的皮尔逊卡方统计量是
(15.3.7)\[\chi^2 = \frac{\sum (y_i - \hat{\mu}_i)}{\hat{\mu}^2}\]
15.3.3. IRLS
IRLS算法是GLM模型参数估计统一框架,适用于所有GLM模型。
牛顿法使用的是观测信息矩阵(OIM),IRLS使用的是期望信息矩阵(EIM)。
IRLS算法参数更新公式为:
(15.3.8)\[\beta^{(t+1)} = (X^T W^{(t)} X)^{-1} X^T W^{(t)} Z^{(t)}\]
我们只需要根据具体的模型去计算出相应的 \(W\) 和 \(Z\) 即可。
权重矩阵 \(W\) 是一个对角矩阵,计算方法如下:
(15.3.9)\[ W^{(t)}
= \text{diag} \left \{ \frac{ 1}{ a(\phi) \nu(\mu) ( g' )^2}
\right \}_{(n\times n)}\]
\(Z\) 是一个列向量,其计算方法如下:
(15.3.10)\[Z^{(t)}= \left \{ (y- \hat{\mu}) g' + \eta^{(t)}
\right \}_{(n\times 1 )}\]
不同的分布拥有不同的 \(a(\phi),\nu(\mu),g\)
,只需按照特定分布提供即可。
这里我们再次给出指数分布的各项内容。
(15.3.11)\[ \begin{align}\begin{aligned}a(\phi) &= 1\\\nu(\mu) &= \mu^2\\g'(\mu) &= \frac{1}{\mu^2}\end{aligned}\end{align} \]
对于规范连接函数的指数分布,其 \(W\) 和 \(Z\) 分别为:
(15.3.12)\[W^{(t)}
= \text{diag} \left \{ \frac{ 1}{ a(\phi) \nu(\mu) ( g' )^2}
\right \}_{(n\times n)}
=\text{diag} \left \{ \hat{\mu}^2 \right \}_{(n\times n)}\]
(15.3.13)\[Z^{(t)} = \left \{ (y- \hat{\mu}) g' + \eta^{(t)}
\right \}_{(n\times 1 )}
= \left \{ \frac{(y- \hat{\mu})}{\hat{\mu}^2} + \eta^{(t)} \right \}_{(n\times 1 )}\]
