离散随机变量的模型中,最常用的是二分类的伯努利模型(逻辑回归模型),
除此外,在本书之前的内容的中,我们已经讨论了很多离散模型,
包括,多分类的类别模型,二项式模型,多项式模型,计数类的泊松分布等等,
甚至还讨论了离散模型特有的一种现象,过度分散问题以及解决的方法。
在众多离散模型中还有一类特殊的情况尚未讨论,那就是有序多分类的场景。
在之前讨论类别分布的多分类模型时说过,类别模型有一个前提假设,
就是类别变量的各个离散状态间是没有顺序相关的,即便通常会用整数值表示每个类别值,
但模型本身是建立在顺序无关的假设之上的。
然而,在实际上应用中这种假设过于强势,
实际场景中存在很多有序的情况,
本章我们针对有序多分类的回归模型进行详细的讨论。
有序的多分类本身也是一个多分类的场景,和类别分布(多项式分布)的区别在于,它允许类别之间存在一定的大小顺序关系。
为什么这里强调多分类,而不说二分类,这是因为对于二分类场景,有序和无序其实没有太差差别,
有序的二分类可以按照无序的二分类来处理。
但是当类别数多余两个时,有序和无序的处理方法就显然不同了。
然而对于有序多分类模型的推导过程,可以看做是二分类逻辑回归模型的扩展,
因此,有序多分类模型也被称为有序逻辑回归模型(ordered logistic regression)。
21.1. 有序逻辑回归
我们先从二分类的场景说起,假设响应变量 \(Y\) 是二值离散变量,
分别用 \(0\) 和 \(1\) 表示 \(Y\) 两个离散状态。
在 GLM 的理论中,协变量(特征变量)向量 \(X\) 和参数向量 \(\beta\)
组成线性预测器 \(\eta=X^T \beta\),响应变量 \(Y\) 的期望 \(\mu\)
和线性预测器 \(\eta\) 之间通过连接函数进行映射。
(21.1.1)\[\eta = g(\mu)\]
线性预测器 \(\eta\) 的取值范围是 \((-\infty,\infty)\)
,如果响应变量 \(Y\) 的两个值 \(0\) 和 \(1\)
之间存在大小(顺序)关系,这里假设 \(0<1\)。
此时可以假设在线性预测器 \(\eta\) 的值域上有一个分割点 \(c\)
,当 \(\eta\) 的值落在区间 \((-\infty,c]\) 时,
响应变量 \(Y=0\)
;反之,当 \(\eta\) 的值落在区间 \((c,\infty)\) 时,
响应变量 \(Y=0\)
。
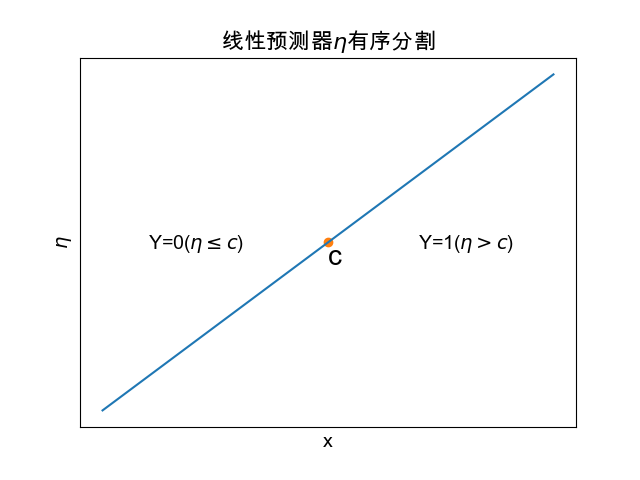
(21.1.2)\[\begin{split}y=
\begin{cases}
0& \text{if}\quad -\infty < \eta <= c\\
1& \text{if} \quad c< \eta < \infty
\end{cases}\end{split}\]
由于变量 \(Y\) 是一个随机变量,不能直接用上面的分段函数输出 \(Y\) 的值
,而是要给出 \(Y\) 的一个概率分布。
假设 \(Y=0\) 的概率和 \(\eta\) 与分割点 \(c\) 的距离(有方向)有关,
\(\eta\) 与分割点 \(c\) 的距离为 \(c-\eta\)
,\(c-\eta\) 越大,\(P(Y=0)\) 也就越大,
\(c-\eta\) 越小,\(P(Y=0)\) 也就越小。
\(c-\eta\) 的值域范围是 \((-\infty,\infty)\)
,而概率值的范围是 \([0,1]\),
因此需要添加一个连接函数对两个空间进行映射。
根据之前的知识,累积概率分布函数可以作为实数域到 \([0,1]\)
的映射函数。
累积概率分布函数有多种选择,比如
logistic ,probit ,clog-log 等等,
这里以 logistic 为例。
\(P(Y=0)\) 可以写成
(21.1.3)\[P(Y=0) =
\frac{e^{c-\eta}}{1+e^{c-\eta}}\]
当 \(\eta\) 趋近于 \(-\infty\) 时,\(c-\eta\) 趋近于 \(+\infty\) ,\(P(Y=0)\) 趋近于 \(1\) 。
当 \(\eta\) 趋近于 \(c\) 时,\(c-\eta\) 趋近于 \(0\) ,\(P(Y=0)\) 趋近于 \(0.5\) 。
当 \(\eta\) 趋近于 \(\infty\) 时,\(c-\eta\) 趋近于 \(-\infty\) ,\(P(Y=0)\) 趋近于 \(0\) 。
\(P(Y=1)\) 可以写为
(21.1.4)\[ \begin{align}\begin{aligned}P(Y=1) &= 1- P(Y=0)\\&= 1 - \frac{e^{c-\eta}}{1+e^{c-\eta}}\\&= \frac{1}{1+e^{c-\eta}}\\&= \frac{e^{ -(c-\eta)}}{1+e^{-(c-\eta)}}\\&= \frac{e^{ \eta-c}}{1+e^{\eta-c}}\end{aligned}\end{align} \]
线性预测器 \(\eta\) 展开为
(21.1.5)\[\eta = x^T\beta=\beta_0 + \beta_1 \times x_1 + \beta_2 \times x_2 +\dots+\beta_p \times x_p\]
\(\eta-c\) 为
(21.1.6)\[ \begin{align}\begin{aligned}\eta-c &= \beta_0 + \beta_1 \times x_1 + \beta_2 \times x_2 +\dots+\beta_p \times x_p -c\\ &= (\beta_0-c) + \beta_1 \times x_1 + \beta_2 \times x_2 +\dots+\beta_p \times x_p\end{aligned}\end{align} \]
虽然 \(\beta_0\) 和 \(c\) 都是未知参数,但是可以把 \((\beta_0-c)\) 看做一个整体并作为截距参数,
\(\beta_0-c \Rightarrow \beta_0\)
,对于模型来说,\(\eta-c\) 和 \(\eta\) 是等价的。
从这里可以看出,在逻辑回归模型中,线性部分的截距 \(\beta_0\) 是和分割点有关的。
最后,利用分割点分方式推导出的逻辑回归和前面章节逻辑回归的定义是等价的。
这意味着有序的二分类逻辑回归模型和传统的无序二分类逻辑回归模型是等价的,
对于二分类来说,有序和无序没有差别。
有序二分类的核心思想就是,在线性预测器 \(\eta\) 的空间中有一个分割点,当 \(\eta\) 的值落在分割点的左侧时,
响应变量 \(Y\) 为 \(0\) 的概率大,
当 \(\eta\) 的值落在分割点的右侧时,
\(Y\) 为 \(1\) 的概率大,
\(Y\) 的概率分布与间距 \(c-\eta\) 正相关,两者可以通过一个累积概率分布函数相连接。
现在我们扩展到多类别(有序)的场景,
假设 \(\eta\) 的整个实数域空间中,有 \(K+1\) 个分割点,
\({c_0,c_1,c_2,\dots,c_K}\)
,并且令 \(c_0=-\infty,c_{K}=+\infty\)
,则整个空间被分成 \(K\) 个段,
分别对应着响应变量 \(Y\) 的 \(K\) 个值。
参考 公式(21.1.2)
,则有
(21.1.7)\[\begin{split}y=
\begin{cases}
1& \text{if}\quad -\infty=c_0 < \eta \le c_1\\
2& \text{if} \quad c_1< \eta \le c_2 \\
3& \text{if} \quad c_2< \eta \le c_3 \\
\vdots \\
K& \text{if} \quad c_{K-1} < \eta < c_K= +\infty
\end{cases}\end{split}\]
假设累积概率分布函数为 \(F\)
,其一阶导数(微分)也就是对应的概率密度(质量)函数用符号 \(f\) 表示
。任意选择一个分割点 \(c_k\) ,
\(F(c_k - \eta)\) 表示响应变量 \(Y\) 小于等于类别 \(k\)
的概率。注意,\(F(c_k - \eta)\) 不是 \(Y=k\) 的概率
,而是 \(Y \le k\) 的概率。
(21.1.8)\[ \begin{align}\begin{aligned}P(Y \le k) &= F(c_k - \eta)\\P(Y > k) &= 1- P(Y \le k) = 1- F(c_k - \eta)\end{aligned}\end{align} \]
\(Y=k\) 的概率可以表示成
(21.1.9)\[ \begin{align}\begin{aligned}P(Y = k) &= P(Y \le k) - P(Y \le k-1)\\&= F(c_k - \eta) - F(c_{k-1} - \eta)\end{aligned}\end{align} \]
特殊的 \(P(Y = 1)\) 和 \(P(Y = K)\) 分别为
(21.1.10)\[ \begin{align}\begin{aligned}P(Y = 1) &= F(c_1 - \eta) - F(c_0 - \eta)\\& = F(c_1 - \eta) - F(-\infty - \eta)\\& = F(c_1 - \eta)\end{aligned}\end{align} \]
(21.1.11)\[ \begin{align}\begin{aligned}P(Y = K) &= F(c_K - \eta) - F(c_{K-1} - \eta)\\& = F(+\infty - \eta) - F(c_{K-1} - \eta)\\& = 1 - F(c_{K-1} - \eta)\\&= 1 - P(Y \le K-1)\end{aligned}\end{align} \]
完整的概率质量函数为
(21.1.12)\[f(y) = \prod_{k=1}^K \left [ F(c_k - \eta) - F(c_{k-1} - \eta) \right ] ^{ \mathbb{I}(y=k)}
,\quad c_0=-\infty,c_{K}=+\infty\]
累计分函数 \(F\) 可以有多种选择,如果是 logistic 函数,就是是有序逻辑回归模型,
如果是高斯累积分布函数就是 probit 有序回归模型,
其它的还有 log-log ,clog-log 等等。
模型的参数除了 \(\beta\) 外,增加了未知参数 \(c^T=[c_1,c_2,\dots,c_{K-1}]\)
,由于参数 \(c\) 替代线性部分的截距参数 \(\beta_0\)
,因此有序多分类模型中的线性部分不再需要解决参数 \(\beta_0\)
。此外注意,所有的类别是共用 \(\beta\) 参数的。
21.2. 参数估计
有序多分类模型同样不能使用 IRLS 算法进行参数估计,需要使用牛顿法等完全最大似然估计。
其对数似然函数为
(21.2.1)\[\ell(y;c,\beta) = \sum_{i=1}^N \sum_{k=1}^K
\mathbb{I}(y_i=k) \ln \left [
F(c_k - \eta_i) - F(c_{k-1} - \eta_i)
\right ]\]
对数似然函数的一阶导数为
(21.2.2)\[\frac{\partial \ell }{\partial \beta_j}
= \sum_{i=1}^N x_{ij} \sum_{k=1}^K
\left [
\frac{-f(c_k - \eta_i) + f(c_{k-1} - \eta_i)}{F(c_k - \eta_i)-F(c_{k-1} - \eta_i)}
\right ]\mathbb{I}(y_i=k)\]
(21.2.3)\[ \begin{align}\begin{aligned}\frac{\partial \ell }{\partial c_k}
&= \sum_{i=1}^N
\left [
\frac{f(c_k - \eta_i)}{F(c_k - \eta_i)-F(c_{k-1} - \eta_i)} \mathbb{I}(y_i=k)
\right.\\&\left. -\frac{f(c_k - \eta_i)}{F(c_{k+1} - \eta_i)-F(c_{k} - \eta_i)} \mathbb{I}(y_i=k+1)
\right ] , 1 \le k \le K-1\end{aligned}\end{align} \]
二阶导数为
(21.2.4)\[ \begin{align}\begin{aligned}\frac{\partial^2 \ell }{\partial \beta_j \partial \beta_t} =
\sum_{i=1}^N x_{ij} x_{it} \sum_{k=1}^K
&\left \{
\frac{f'(c_k - \eta_i) - f'(c_{k-1} - \eta_i)}{F(c_k - \eta_i)-F(c_{k-1} - \eta_i)}
\right.\\&\left. -\frac{ [-f(c_k - \eta_i) + f(c_{k-1} - \eta_i) ]^2 }{ [ F(c_k - \eta_i)-F(c_{k-1} - \eta_i)]^2 }
\right \}\mathbb{I}(y_i=k)\end{aligned}\end{align} \]
(21.2.5)\[\frac{\partial^2 \ell }{\partial c_k \partial c_t}
= - \sum_{i=1}^N
\frac{f(c_k - \eta_i)f(c_t - \eta_i)}{ [ F(c_k - \eta_i)-F(c_{t} - \eta_i)]^2 }
\mathbb{I}(y_i=\mathop{max}(k,t)) \mathbb{I}(|k-t|=1)\]
(21.2.6)\[ \begin{align}\begin{aligned}\frac{\partial^2 \ell }{\partial c_k \partial c_k}
&= \sum_{i=1}^N \big \{\\&\left [
\frac{f'(c_k-\eta_i)}{F(c_k-\eta_i)-F(c_{k-1}-\eta_i)}
-\frac{f(c_k-\eta_i)[ f(c_k-\eta_i) -f(c_{k-1}-\eta_i) ] }{ [F(c_k-\eta_i)-F(c_{k-1}-\eta_i)]^2 }
\right ]\mathbb{I}(y_i=k)\\-&\left [
\frac{f'(c_k-\eta_i)}{F(c_{k+1}-\eta_i)-F(c_{k}-\eta_i)}
-\frac{f(c_k-\eta_i)[ f(c_{k+1}-\eta_i) -f(c_{k}-\eta_i) ] }{ [F(c_{k+1}-\eta_i)-F(c_{k}-\eta_i)]^2 }
\right ]\mathbb{I}(y_i=k+1)\\&\big \}\end{aligned}\end{align} \]
(21.2.7)\[\frac{\partial^2 \ell }{\partial c_k \partial \beta_t} =
- \sum_{i=1}^N [
x_{it} \mathcal{A}_i \mathbb{I}(y_i=t)
- \mathcal{B}_i \mathbb{I}(y_i=t+1)\]
其中
(21.2.8)\[ \begin{align}\begin{aligned}\mathcal{A}_i &= \frac{ f(c_k-\eta_i) [F(c_k-\eta_i)-F(c_{k-1}-\eta_i) +f(c_k-\eta_i)-f(c_{k-1}-\eta_i) ]}
{[F(c_k-\eta_i)-F(c_{k-1}-\eta_i)]^2}\\\mathcal{B}_i &= \frac{ f(c_k-\eta_i) [F(c_{k+1}-\eta_i)-F(c_{k}-\eta_i) +f(c_{k+1}-\eta_i)-f(c_{k}-\eta_i) ]}
{[F(c_{k+1}-\eta_i)-F(c_{k}-\eta_i)]^2}\end{aligned}\end{align} \]
21.3. 连接函数
现在,我们讨论下有序多分类模型常用的连接函数。
上一节中,用符号 \(F\) 表示累积分布函数,
符号 \(f\) 表示 \(F\) 的导数,也就是累积分布函数对应的概率密度函数。
\(F\) 的作用就类似于逻辑回归模型中的响应函数,
\(F\) 的反函数就是连接函数。
有序多分类模型可以看做逻辑回归模型的一种扩展,
因此逻辑回归模型的连接函数在有序多分类模型中都可以使用。
21.3.1. logit
logistic 函数是 logit 函数的反函数,
它同时也是标准逻辑分布(standard logistic distribution)的累积分布函数。
当累积分布函数 \(F\) 采用 logistic
函数时,就相当于采用 logit 连接函数。
(21.3.1)\[F(a) = \frac{\exp(a) }{1+\exp(a)}\]
(21.3.2)\[ \begin{align}\begin{aligned}f(a) &= F'(a)\\&= \frac{\exp(a) }{[1+\exp(a)]^2}\\&= F(a)[1-F(a)]\end{aligned}\end{align} \]
(21.3.3)\[ \begin{align}\begin{aligned}f'(a) &=\frac{\exp(a) - \exp{ (2a) } }{[1+\exp(a)]^3}\\&= F(a)[1-F(a)]\{ F(a)-[1-F(a)] \}\end{aligned}\end{align} \]
21.3.2. probit
当 \(F\) 采用累积正态分布时,就是 probit 模型,
用符号 \(\Phi\) 表示累积正态分布函数,
符号 \(\phi\) 表示正态分布的概率密度函数。
(21.3.4)\[ \begin{align}\begin{aligned}F(a) &= \Phi(a)\\f(a) &= \phi(a)\\f'(a) &= -a\phi(a)\end{aligned}\end{align} \]
21.3.3. clog-log
clog-log 连接函数的反函数是广义耿贝尔分布(generalized Gumbel distribution )的累积分布函数。
\(F\) 也可以是 clog-log 函数反函数。
(21.3.5)\[ \begin{align}\begin{aligned}F(a) &= 1 - \exp\{ -\exp(a) \}\\f(a) &= [ F(a)-1] \ln [ 1- F(a)]\\f'(a) &= f(a) \{ 1+\ln[1-F(a) ] \}\end{aligned}\end{align} \]
21.3.4. log-log
当 \(F\) 是 log-log 反函数时,有
(21.3.6)\[ \begin{align}\begin{aligned}F(a) &= \exp\{ -\exp(-a) \}\\f(a) &= - F(a) \ln [ F(a)]\\f'(a) &= f(a) \{ 1+\ln[F(a) ] \}\end{aligned}\end{align} \]
21.3.5. cauchit
柯西分布(Cauchy distribution )的定义域也是整个实数域,
因此柯西分布的累积分布函数也可以拿来用。
当响应函数 \(F\) 是标准柯西分布的累积分布函数时,
连接函数称为 cauchit
。
(21.3.7)\[ \begin{align}\begin{aligned}F(a) &= 0.5 + \pi^{-1} atan(-a)\\f(a) &= -\frac{1}{\pi(1+a^2)}\\f'(a) &= f(a) 2\pi a\end{aligned}\end{align} \]
