18. 分类模型

本章我们讨论分类模型，分类模型和回顾模型的区别是，标签变量 \(Y\) 的取值空间是一个有限集合，一个小小的变化拥有着重大的意义。 当 \(Y\) 的取值为有限个时，我们可以将其看做标签(label)或者类别(class)，可以当做是未一个输入 \(x\) 打上一个类别标签 \(y\) ， 也可以理解成是把输入样本数据分成 \(|Y|\) 个类别，所以称之为分类问题。

在分类问题中，通常把输入样本数据 \(X\) 称为 特征向量(feature vector) ，离散变量 \(Y\) 称为 类别标签(class label) 。 依据类别标签 \(Y\) 的取值个数，分类模型可以分为二分类和多分类。 当类别标签 \(Y\) 只有两个取值时，称为二分类问题，这时我们把变量 \(Y\) 当做伯努利变量。 当类别标签 \(Y\) 拥有两个以上的值时，称为多分类问题，这时我们把变量 \(Y\) 当做多项式变量。

无论是回归问题，还是分类问题，核心的问题都是对条件概率分布 \(P(Y|X)\) 进行建模， 在分类问题中有两种建模方法， 一种称为生成式(generative)方法，一种称为判别式(discriminative)方法。 生成式是通过贝叶斯定理进行建模，而判别式是直接为 \(P(Y|X)\) 选取一个合适的函数，这和回归模型很类似，稍后我们会详细讨论两种方式的差异。

18.1. 生成模型与判别模型

我们已经知道机器学习模型的本质就是要找到一个最优的条件概率分布 \(p(Y|X)\) ， 在分类问题中，要对条件概率分布 \(p(Y|X)\) 进行建模，一般有两种方法。 一种是直接选用一个参数化的函数模型表示条件概率分布，比如：

(18.1.11)\[p(y|x) = D(x;\theta)\]

函数 \(D(x;\theta)\) 可以称为判别函数(discriminative function)，也可以称为决策函数， 这样的模型被称为判别模型(discriminative model)。 其中 \(\theta\) 是模型参数，输入一个样本的特征 \(x\) ， 直接输出模型的预测结果。 判别模型是直接对条件概率 \(p(Y|X)\) 进行建模，然后利用训练数据和参数估计算法估计出判别函数的未知参数 \(\theta\) ， 比如逻辑回归模型。

另一种模型建模方法是利用贝叶斯定理进行建模，将条件概率 \(p(Y|X)\) 转换成类别先验概率 \(p(Y)\) 和 类别条件概率 \(p(X|Y)\) 。

(18.1.12)\[p(y|x) = \frac{p(y)p(x|y)}{p(x)} = \frac{p(y)p(x|y)}{\int p(y)p(x|y) dy }\]

这类模型被称为 生成模型(generative model) 。 生成模型是直接对类别先验概率 \(p(Y)\) 和类别条件概率 \(p(X|Y)\) 进行建模， 为二者选取合适的参数化概率分布模型，然后利用训练数据估计出其中的参数。这类模型中比较典型的时朴素贝叶斯模型。

判别模型中，特征变量 \(X\) 是类别变量 \(Y\) 的父结点， 然而在生成模型中，是把类别变量 \(Y\) 看成特征变量 \(X\) 的父结点。

图 18.1.8 (a)生成式模型的图形表示。生成模型需要对边缘概率 \(p(y)\) 以及条件概率 \(p(x|y)\) 进行建模。 (b)判别式模型的图形表示。判别模型直接对条件概率 \(p(y|x)\) 进行建模。

18.2. 线性回归与线性分类

一个离散变量可以看成是特殊的连续值(实数值)变量，那么我们是否可以用回归模型来解决分类问题呢？ 然而，这样做是存在很大问题的，我们举例说明下。

为了直观理解，我们简化为只有一个特征变量 \(X\) 的二分类问题，我们把类别变量 \(Y\) 看成一个连续值变量，其取值范围是 \(Y\in[0,1]\) ，其中 \(Y=0\) 和 \(Y=1\) 分别表示两个类别。如 图 18.2.1 所示，纵轴表示y，横轴表示特征变量值，图中的点表示两类样本。 两类样本泾渭分明，分别为 \(Y=0\) 类别 和 \(Y=1\) 类别。 图中的直线是拟合这些样本的回归线，我们把这条线的y值看做是样本属于类别1的概率 \(p(Y=1|X)=y\) 。

图 18.2.1 用回归线拟合二分类样本。横坐标是一维特征 \(X\) ，纵坐标表示二分类标签 \(Y\) ，直线是最小均方线性回归拟合线。

然而，这条拟合线的y值会超出范围 \([0,1]\) ，使得在二分类场景下不具备准确的概率解释。 除此之外还存在更多问题，假设我们向数据集中增加一个新的样本点(1.5,1)，如 图 18.2.2 ， 原来的拟合线( 图 18.2.1 )，在 \(x=1.5\) 时输出值2.01，不管选择什么样的分类阈值，这个样本都会被分为类别1。

图 18.2.2 三条最小均方回顾拟合线。

18.3. 生成模型

在实际的应用中，通常会有多个特征变量，这些特征变量形成一个特征向量 \(X\) ， 当我们对 \(p(X|Y)\) 进行建模时，就要考虑到特征变量之间的关系，特征变量之间的关系可以分成三种情况， 如 图 18.3.2 所示，在这这三种情况下，类别变量结点 \(Y\) 都是特征向量 \(X=(X_1,X_2,\dots,X_m)\) 的父结点。

1. 完全独立模型。如 图 18.3.2 (a)所示，特征变量都是相互独立的的结点，这种情况下子结点间在 \(Y\) 的条件下相互独立， 也就是任意两个特征变量间满足条件独立性 \(X_i \perp \!\!\! \perp X_j | Y,i \ne j,(i,j)\in [1,m]\) 。

2. 部分独立模型。如 图 18.3.2 (b)所示，特征变量间存在局部内部依赖，特征结点可以分成几个子集合，每个子集合内存在依赖关系， 子集合与子集合之间存在条件独立性。

3. 完全依赖性。如 图 18.3.2 (c)所示，在这种模型中，特征变量间不存在任何条件独立性。 这种情况下我们把特征向量用一个结点表示，尽管看上去图表示上更简单了，但是它是三种模型中最具备普适性的。 本节我们会讨论这种模型的一个例子，其类别条件概率密度假设为高斯分布。

图 18.3.2 (a)特征变量间完全条件独立的模型； (b)特征变量间部分条件独立的模型； (c)特征变量间条件不独立的模型

本节我们重点讨论第一种生成模型，即特征变量间是完全的条件独立的， 在所有例子中，我们的讨论都包括两部分：(1)后验概率 \(p(y|x)\) 的参数化表示；(2)模型参数的最大似然估计。

18.3.1. 高斯判别模型

现在我们讨论 图 18.3.2 (a) 的一个分类模型，这里模型中特征变量之间存在完全的条件独立。 这里假设特征变量都是连续值随机变量，并且每个特征 \(p(X_j)\) 都符合高斯分布， 这时我们就可以假设条件概率分布 \(p(X_j|Y)\) 为高斯分布。 因为我们用高斯分布表示条件概率 \(p(X_j|Y)\) ，所以称为高斯判别(Gaussian Discriminant)模型， 虽然名字中有”判别(Discriminant)”两个字，但它是生成模型。

类别边缘概率

在生成模型中，我们需要为类别边缘概率 \(p(Y)\) 和 类别条件概率 \(p(X|Y)\) 进行建模。 我们先从二分类问题开始，即类别变量 \(Y\) 是伯努利变量，取值为0或1，代表两个类别。 稍后再讨论多分类问题。 令 \(Y\) 是伯努利分布，其参数是 \(\lambda\) 。

(18.3.13)\[p(y;\lambda) = \lambda^y(1-\lambda)^{1-y}\]

类别条件概率

给定 图 18.3.2 (a) 的条件独立性假设，条件概率分布 \(p(X|Y)\) 可以分解为多个条件概率分布 \(p(X_j|Y)\) 的乘积。 对于 \(Y=0\) ，令每一个特征变量 \(X_j\) 为一个高斯分布：

(18.3.14)\[p(x_j|Y=0;\theta_j) = \frac{1}{ (2\pi\sigma_j^2)^{1/2} } \exp \left \{ - \frac{1}{2\sigma_j^2}(x_j-\mu_{0j})^2 \right \}\]

其中 \(\mu_{0j}\) 表示当类别为 \(Y=0\) 时，第j个特征变量的高斯分布的均值参数。 同理，对于类别 \(Y=1\) ，有

(18.3.15)\[p(x_j|Y=1;\theta_j) = \frac{1}{ (2\pi\sigma_j^2)^{1/2} } \exp \left \{ - \frac{1}{2\sigma_j^2}(x_j-\mu_{1j})^2 \right \}\]

注意，对于同一个特征变量 \(X_j\) ，\(Y=0\) 与 \(Y=1\) 条件下的高斯分布拥有相同的方差参数 \(\sigma_j^2\) ，不同均值参数 \(\mu_{0j}\) 和 \(\mu_{1j}\) 。 为了方便表示，我们定义 \(\theta_j=\{\mu_{0j},\mu_{1j},\sigma_j^2\}\) 表示特征变量 \(X_j\) 的所有参数。

联合概率

模型的联合概率可以写成如下形式，因为特征变量之间关于变量 \(Y\) 条件独立，所以 \(p(X|Y)=\prod_{j=1}^{m}p(x_j|y;\theta_j)\) ：

(18.3.16)\[p(x,y;\theta) = p(y;\lambda) \prod_{j=1}^{m}p(x_j|y;\theta_j)\]

其中定义 \(\theta=\{\lambda,\theta_1,\theta_2,\dots,\theta_m \}\) 。

后验概率

现在我们计算后验概率 \(p(Y=1|x;\theta)\) 。 为了推导方便， 我们用符号 \(\Sigma\) 表示特征变量协方差矩阵，我们的特征变量 \(X\) 是一个向量，可以用一个多维高斯分布表示类别条件概率：

(18.3.17)\[p(x|y=k;\theta)=\frac{1}{(2\pi)^{1/2} {|\Sigma|}^{1/2} } \exp \left \{ -\frac{1}{2}(x-\mu_k)^T \Sigma^{-1} (x-\mu_k) \right \}\]

对于每个类别 \(k \in \{0,1\}\) ，其中 \(\mu_k \triangleq (\mu_{k1},\mu_{k2},\dots,\mu_{km})\) 为第k个高斯分布的均值向量。

备注

在统计学与概率论中，协方差矩阵（也称离差矩阵、方差-协方差矩阵）是一个矩阵， 其 \(i,j\) 位置的元素是第 \(i\) 个与第 \(j\) 个随机变量之间的协方差。 协方差描述的是两个变量之间的相关性，如果两个变量是正相关，协方差大于0；如果两个变量是负相关，协方差小于0； 如果两个变量不相关，协方差为0。协方差矩阵对角线的元素 \(\Sigma[ii]\) 表示的是变量 \(X_i\) 的方差，即 \(\Sigma[ii]=\sigma_i^2\) 。

在这里，由于特征变量之间关于变量 \(Y\) 条件独立的，所以协方差矩阵 \(\Sigma\) 应该是一个对角矩阵 \(\Sigma \triangleq diag(\sigma^2_1,\sigma^2_2,\dots,\sigma^2_m)\) ，对角线的元素是每个变量的方差，其它元素都是0。

现在讨论下特征变量间方差的关系，如 图 18.3.3 所示， 假设只有两个特征 \(x_1\) 和 \(x_2\) ， 每幅图中右上角的同心圆表示类别 \(Y=1\) 的条件下的高斯分布的轮廓图， 左下角的同心圆表示类别 \(Y=0\) 的条件下的高斯分布的轮廓图， 注意两个类别条件的高斯分布有相同的方差参数，所以同一幅图中两组同心圆形状是相同的。 我们用 \(\sigma_1\) 表示高斯分布 \(p(x_1|y;\sigma_1)\) 的方差， \(\sigma_2\) 表示高斯分布 \(p(x_2|y;\sigma_2)\) 的方差。 当 \(\sigma_1=\sigma_2\) 时，我们看到是(a)图，同心圆是正圆， 当 \(\sigma_1 \ne \sigma_2\) 时，我们看到是(b)图，同心圆是椭圆。

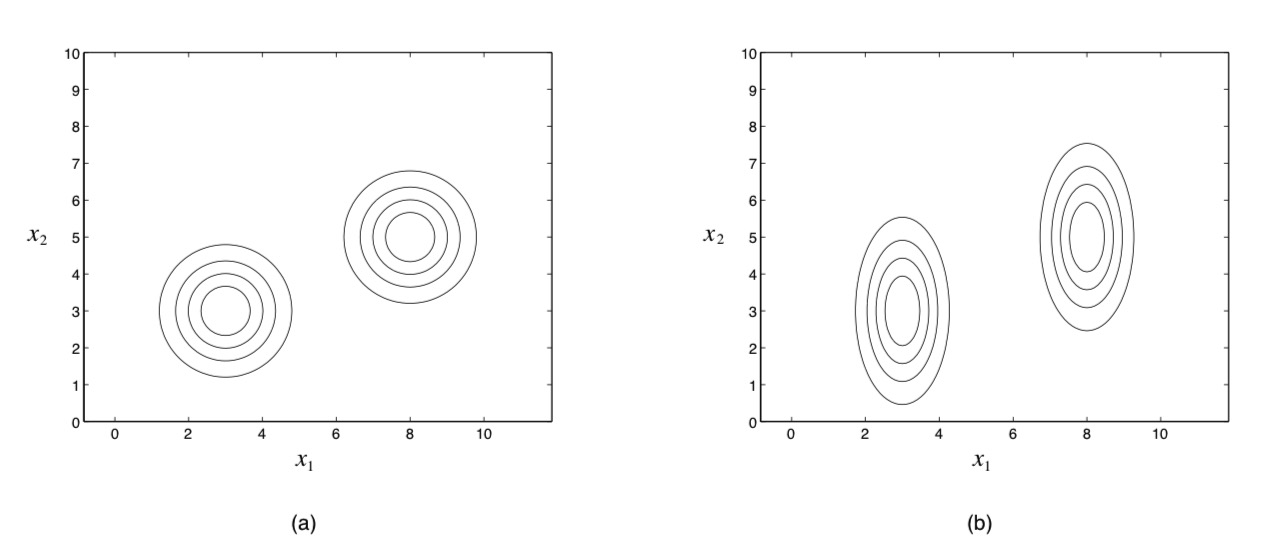
图 18.3.3 (a)方差为 \(\sigma_1=1,\sigma_2=1\) 的高斯类别条件密度的轮廓图； (b)方差为 \(\sigma_1=0.5,\sigma_2=2.0\) 的高斯类别条件密度的轮廓图；

类别变量的后验概率分布为：

(18.3.18)\[ \begin{align}\begin{aligned}p(Y=1|x;\theta) &= \frac{p(Y=1;\lambda) p(x|Y=1;\theta)} {p(x|Y=1;\theta)p(Y=1;\lambda) +p(x|Y=0;\theta)p(Y=0;\lambda) }\\ &= \frac{\lambda \exp \{ -\frac{1}{2} (x-\mu_1)^T\Sigma^{-1}(x-\mu_1) \} } { \lambda \exp \{ -\frac{1}{2} (x-\mu_1)^T\Sigma^{-1}(x-\mu_1) \} + (1-\lambda) \exp \{ -\frac{1}{2} (x-\mu_0)^T\Sigma^{-1}(x-\mu_0) \} }\\ &= \frac{1}{1+ \exp \{ -log \frac{\lambda}{1-\lambda} + \frac{1}{2}(x-\mu_1)^T\Sigma^{-1}(x-\mu_1) - \frac{1}{2} (x-\mu_0)^T\Sigma^{-1}(x-\mu_0) \} }\\&=\frac{1}{1+\exp \{ -(\mu_1-\mu_0)^T\Sigma^{-1}x +\frac{1}{2}(\mu_1-\mu_0)^T\Sigma^{-1}(\mu_1+\mu_0) - \log \frac{\lambda}{1-\lambda}\} }\\ &= \frac{1}{1+\exp\{ -\beta^Tx-\gamma \}}\end{aligned}\end{align} \]

其中最后一个等式，我们定义了两个新参数 \(\beta\) 和 \(\gamma\) 来简化公式。

(18.3.19)\[ \begin{align}\begin{aligned}\beta &\triangleq \Sigma^{-1}(\mu_1-\mu_0)\\\gamma &\triangleq -\frac{1}{2}(\mu_1-\mu_0)^T\Sigma^{-1}(\mu_1+\mu_0) + \log \frac{\lambda}{1-\lambda}\end{aligned}\end{align} \]

我们发现 \(Y=1\) 的后验概率拥有如下的特殊形式：

(18.3.20)\[\phi(z) \triangleq \frac{1}{1+e^{-z}}\]

其中 \(z=\beta^Tx+\gamma\) 是x的仿射函数，函数 \(\phi(z)\) 是一个平滑的S型曲线， 通常称之为 逻辑函数(logistic function) ，也被称为sigmod函数 (如 图 18.3.4 )。

备注

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

图 18.3.4 逻辑函数的曲线

图 18.3.5 图中虚线和实线都是等后验概率的轮廓线， (a)当 \(\sigma_1 = \sigma_2\) ，这些等线正交于两个类别的均值向量间的连线。 (b)当 \(\sigma_1 \ne \sigma_2\) ，后验概率等轮廓线仍然是直线，但是他们不再正交于均值向量的连线。

现在我们探讨一下后验概率的几何解释，如 图 16.3.2 所示。 特征向量 \(x\) 通过一个仿射函数线性变换成 \(z\) ， 然后再经过sigmod函数 \(\phi(z)\) 得到后验概率值。 仿射函数 \(z=\beta^Tx+\gamma\) 的 \(\beta^Tx\) 在几何上表示特征向量 \(x\) 到 \(\beta\) 向量上的投影， 而向量 \(\beta\) 和两个类别高斯的均值相关。

(18.3.21)\[\beta \triangleq \Sigma^{-1} (\mu_1-\mu_0)\]

其中 \(\mu_1-\mu_0\) 两个均值向量的差值，图 16.3.2 中两组同心圆的连线。 协方差矩阵 \(\Sigma\) 是一个对角矩阵，我们假设所有特征的方差相同，即协方差矩阵 \(Sigma\) 对角元素都相等，我们假设方差都为1，即协方差矩阵为单位矩阵 \(\Sigma=I\) ， 这时 \(\beta=(\mu_1-\mu_0)\) 。 此时在特征空间中，特征向量 \(x\) 到 \(\beta\) 的投影就是：

(18.3.22)\[\beta^T x = (\mu_1-\mu_0)^T x\]

此时，所有落在正交于 \(\beta\) 的直线上的特征向量 \(x\) 的投影都是相等的， 图 16.3.2 (a)中斜直线。 \(z\) 的 \(\gamma\) 部分与 \(x\) 无关，对于特征空间中的所有 \(x\) ， \(\gamma\) 部分都是一样的值， 所以投影相同意味着 \(z\) 相同，\(z\) 相同意味着后验概率 \(\phi(z)\) 相同。 特征空间中，同一条斜直线上的特征点，其后验概率相同。 换句话说，这些斜直线是等后验概率轮廓线。

再来看一个特殊的情况，当两个类别的先验概率相同 \(\lambda=1-\lambda\) 时， \(z=0\) 中的子项 \(log(\lambda/(1-\lambda))\) 就会被消除掉。 这时 \(z\) 可以改写成：

(18.3.23)\[ \begin{align}\begin{aligned}z&= (\mu_1-\mu_0)^T\Sigma^{-1}x - \frac{1}{2}(\mu_1-\mu_0)^T\Sigma^{-1}(\mu_1+\mu_0)\\&=(\mu_1-\mu_0)^T\left ( x-\frac{(\mu_1+\mu_0)}{2} \right )\end{aligned}\end{align} \]

此时，当 \(x=\frac{(\mu_1+\mu_0)}{2}\) 时，有 \(z=0\) 。 进而有 \(p(Y=1|x)=p(Y=0|x)=0.5\) ，这是因为当 \(z=0\) 时， 逻辑函数的值为0.5，两个类别的后验概率相等，图 16.3.2 中的实斜线， 实斜线代表的是后验概率等于0.5的位置。

类别变量的先验参数 \(\lambda\) 通过 对数几率比(log odds ratio) \(log(\lambda/(1-\lambda))\) 影响着后验概率，这一项可以看成 图 18.3.4 横轴上的平移。 当 \(\lambda\) 大于0.5时，会使得图像向左平移，后验概率 \(p(Y=1|x)\) 得到一个较大的的值， 参考 图 16.3.3 (a)。 反之，当 \(\lambda\) 小于0.5时，相当于图像右移，参考 图 16.3.3 (b)。

图 18.3.6 每个图中右上角的图形是类别 \(Y=1\) 条件下的高斯，左下角是类别 \(Y=0\) 的高斯。 (a)当类别先验 \(\lambda\) 大于0.5时，等后验概率轮廓线向左移动，得到的后验概率更倾向于类别 \(Y=1\) 。 (b)当类别先验 \(\lambda\) 小于0.5时，等后验概率轮廓线向右移动，得到的后验概率更倾向于类别 \(Y=0\) 。

我们额外增加一个新的特征，其值为固定值1，\(x=[x^{old},1]\) ， 并且定义 \(\theta \triangleq (\gamma-log(\lambda/(1-\lambda)),\beta)^T\) ， \(\theta\) 是一个关于 \(\mu_k,\Sigma,\lambda\) 的函数。 用这些新的符号改写一下后验概率可得：

(18.3.24)\[p(Y=1|x;\theta) = \frac{1}{1+e^{-\theta^Tx}}\]

经过简化后我们发现，类别条件高斯密度的后验概率是特征向量 \(x\) 的线性函数外套上一个的逻辑函数。 我们得到了一个 线性分类(linear classifier)器 ，”线性”的含义是：特征空间的等后验概率轮廓线是直线。 事实上，如果直接用这个函数进行分类建模，就是我们常说的逻辑回归(logistics regression)模型。

重要

高斯判别模型是建立在很多假设的基础上的，(1)特征变量关于类别变量完全条件独立 \(X_i \perp \!\!\! \perp X_j | Y,(i,j)\in [1,m]\) 。 (2) 特征变量 \(X_j\) 服从高斯分布。 (3 )两个类别的条件高斯分布具有相同的协方差矩阵，类别1的条件高斯分布 \(p(X|Y=1;\mu_0,\Sigma)\) 和类别0的条件高斯分布 \(p(X|Y=0;\mu_1,\Sigma)\) 就有不同的均值参数，相同的协方差参数。 这三个建设任意一个不满足时，高斯判别模型就不适用。

其中一个假设是两个类别的条件高斯分布的协方差参数是相同的，这个假设使得后验概率的分子分母中的 二次项 \(x^T\Sigma^{-1}x\) 被消除掉。 如果我们取消了这个假设，后验概率仍然是逻辑函数的形式，但是逻辑函数内会包含特征 \(x\) 的二次项， 这时，等后验概率的轮廓线将不再是直线，而是二次曲线，得到的分类器将是二次分类器(quadratic classifier)。

最大似然估计

现在我们讨论如何用最大似然估计估计出模型的参数，假设我们有规模为N的训练数据集 \(\mathcal{D}=\{(x_m,y_m);n=1,\dots,N \}\) 。 假设我们把数据集分成两份，一份是 \(y_n=0\) 的样本，另一份是 \(y_n=1\) 的样本。 则对数似然函数为

(18.3.25)\[ \begin{align}\begin{aligned}\ell(\theta;\mathcal{D}) &= \log \left \{ \prod_{n=1}^N \left [ p(y_n;\lambda) \prod_{j=1}^m p(x_{j,n}|y_n;\theta_j) \right ] \right \}\\&= \sum_{n=1}^N log p(y_n;\lambda) + \sum_{n=1}^N \sum_{j=1}^m p(x_{j,n}|y_n;\theta_j)\end{aligned}\end{align} \]

对数似然函数被分割成两部分，两部分的参数是独立的，可以分开各自进行极大化求解。 一部分是 \(Y\) 的边缘概率分布，另一部分是给定 \(Y\) 的条件概率分布。 我们先极大化前者，估计参数 \(\lambda\) 。

(18.3.26)\[ \begin{align}\begin{aligned}\hat{\lambda}_{ML} &= \mathop{\arg \max}_{\lambda} \sum_{n=1}^N \log p(y_n;\lambda)\\&= \mathop{\arg \max}_{\lambda} \sum_{n=1}^N \{ y_n \log \lambda +(1-y_n)log(1-\lambda)\end{aligned}\end{align} \]

类别变量先验概率分布是一个伯努利分布，我们知道伯努利分布参数 \(\lambda\) 的最大似然估计值就是经验分布， 也即是样本中 \(y_n=1\) 的比例。

(18.3.27)\[\hat{\lambda}_{ML}=\frac{\sum_{n=1}^N y_n}{N}\]

\(\sum_{n=1}^N y_n\) 的值就是在N条样本中 \(Y=1\) 的样本数量。

现在我们最大化第二项求解高斯分布的参数，第二项进一步展开：

(18.3.28)\[ \begin{align}\begin{aligned}\sum_{n=1}^N \sum_{j=1}^m p(x_{j,n}|y_n;\theta_j) &= \sum_{n=1}^N \sum_{j=1}^m \log \{ p(x_{j,n}|y_n=1;\mu_{j1},\sigma_j)^{y_n} p(x_{j,n}|y_n=0;\mu_{j0},\sigma_j)^{1-y_n} \}\\&= \sum_{j=1}^m \left \{ \sum_{n=1}^N y_n \log p(x_{j,n}|y_n=1;\mu_{j1},\sigma_j) + \sum_{n=1}^N (1-y_n)p(x_{j,n}|y_n=0;\mu_{j0},\sigma_j) \right \}\end{aligned}\end{align} \]

观测上式可以发现，对于每个特征j其参数为 \(\theta_j=\{ \mu_{j0},\mu_{j1},\sigma_j \}\) ， 上式可以分成m部分，每个部分是一个特征的参数，不同特征的参数是相互独立的，可以分开进行估计。

(18.3.29)\[\hat{\theta}_{j,ML} = \mathop{\arg \max}_{\theta_j} \sum_{n=1}^N y_n \log p(x_{j,n}|y_n=1;\mu_{j1},\sigma_j) + \sum_{n=1}^N (1-y_n)p(x_{j,n}|y_n=0;\mu_{j0},\sigma_j)\]

这个公式又是分为两项，每个类别是一项，其中 \(\mu_{j1}\) 只和第一项有关， 参考 节 2.1.3 讲过的 高斯分布的最大似然估计，我们去掉常数项。

(18.3.30)\[ \begin{align}\begin{aligned}\hat{\mu}_{j1,ML} &= \mathop{\arg \max}_{\theta_j} \sum_{n=1}^N y_n \log p(x_{j,n}|y_n=1;\mu_{j1},\sigma_j)\\&= \sum_{n=1}^N y_n \log \left [ \frac{1}{ (2\pi\sigma_j^2)^{1/2} } \exp \left \{ - \frac{1}{2\sigma_j^2}(x_j-\mu_{1j})^2 \right \} \right ]\\ &= \sum_{n=1}^N y_n \log \frac{1}{ (2\pi\sigma_j^2)^{1/2} } - \sum_{n=1}^N y_n \frac{1}{2\sigma_j^2}(x_j-\mu_{1j})^2\\&\triangleq - \sum_{n=1}^N y_n (x_j-\mu_{1j})^2\end{aligned}\end{align} \]

这等价于一个加权最小均方(weighted least-squares)问题，其中的权重(weights)是二值变量 \(y_n\) 。 求导并令导数为零，可得：

(18.3.31)\[\hat{\mu}_{j1,ML} = \frac{\sum_{n=1}^N y_n x_{j,n}}{\sum_{n=1}^N y_n}\]

这个式子可以理解成：所有 \(Y=1\) 的样本中 \(x_j\) 的均值就是 \(\hat{\mu}_{j1,ML}\) 。 同理，对于 \(Y=0\) 时：

(18.3.32)\[\hat{\mu}_{j0,ML} = \frac{\sum_{n=1}^N (1-y_n) x_{j,n}}{\sum_{n=1}^N (1-y_n)}\]

最后，方差的最大似然估计结果为：

(18.3.33)\[\hat{\sigma}^2_{j,ML} = \frac{\sum_{n=1}^N y_n(x_{j,n}-\hat{\mu}_{j1,ML})^2}{\sum_{n=1}^N y_n} + \frac{\sum_{n=1}^N (1-y_n)(x_{j,n}-\hat{\mu}_{j0,ML})^2}{\sum_{n=1}^N (1-y_n)}\]

多分类

我们已经讨论完二分类的高斯判别模型，现在我们讨论下在多分类场景下的高斯判别模型。 在二分类问题中，我们假设类别变量为伯努利变量 \(Y \in {0,1}\) 。 显然在多分类的场景中，类别变量 \(Y\) 将不再是伯努利变量，而是一个多项式变量。 我们假设一共有K个类别，即类别变量 \(Y\) 是一个K值多项式变量， 我们用one-hot方法表示变量 \(Y\) ，用一个K维的向量表示变量 \(Y\) 的取值， \(y=[\lambda_1,\lambda_2,\dots,\lambda_K], \sum_{k=1}^K \lambda_k = 1\) ， 其中 \(\lambda_k\) 表示向量的第k个元素为1的概率，也就是多项式变量 \(Y\) 是第k个类别的概率。

(18.3.34)\[\lambda_k=p(Y^k=1;\lambda)\]

其中 \(Y^k\) 表示类别向量的第k个元素。多项式变量 \(Y\) 的概率质量函数可以写成：

(18.3.35)\[p(y;\lambda) = \prod_{k=1}^K \lambda_k^{\delta(y,y_k)}\]

其中 \(\delta(y,y_k)\) 是指示函数，当 \(y=y_k\) 成立的时候值为1，否则值为0。 同样，对于每种类别k，定义一个条件高斯密度函数：

(18.3.36)\[p(x|Y^k=1;\theta)=\frac{1}{(2\pi)^{1/2}|\Sigma|^{1/2}} \exp \left \{ -\frac{1}{2}(x-\mu_k)^T \Sigma^{-1} (x-\mu_k) \right \}\]

其中 \(\mu_k\) 是第k个类别下特征变量高斯分布的均值参数，\(\Sigma\) 是方差参数。 和之前二分类高斯判别模型一样，仍然假设所有类别下特征变量的高斯分布拥有同一个方差参数 \(\Sigma\) 。 又因为在给定 \(Y\) 时，所有特征变量是相互条件独立的( 图 18.3.2 (a))，所以协方差矩阵 \(\Sigma\) 是一个对角矩阵。 对于更一般的协方差矩阵 \(\Sigma\) (不是对角矩阵)，就意味着是 图 18.3.2 (c) 所示的模型，特征变量间不满足条件独立性。

根据贝叶斯定义可以得到类别k的后验概率：

(18.3.37)\[ \begin{align}\begin{aligned}p(Y^k=1|x;\theta) &= \frac{p(Y^k=1;\lambda) p(x|Y^k=1;\theta) } { \sum_{l=1}^{K} p(Y^l=1;\lambda) p(x|Y^l=1;\theta) }\\&= \frac{ \lambda_k \exp \{ -\frac{1}{2}(x-\mu_k)^T\Sigma^{-1}(x-\mu_k) \} } {\sum_{l=1}^{K} \lambda_l \exp \{ -\frac{1}{2}(x-\mu_l)^T\Sigma^{-1}(x-\mu_l) \} }\\&= \frac{ \exp \{ \mu_k^T\Sigma^{-1}x -\frac{1}{2} \mu_k^T \Sigma^{-1}\mu_k + \log \lambda_k \}} { \sum_{l=1}^{K} \exp \{ \mu_l^T\Sigma^{-1}x -\frac{1}{2} \mu_l^T \Sigma^{-1}\mu_l + \log \lambda_l \}}\end{aligned}\end{align} \]

计算过程中，x的二次项 \(x^T\Sigma^{-1}X\) 可以被消除掉，使得最后得到的是x的线性函数的指数。 我们定义一个新的参数 \(\beta_k\) 简化上述公式。

(18.3.38)\[\begin{split}\beta_k \triangleq \left [ \begin{matrix} -\mu_k^T \Sigma^{-1} \mu_k + \log \lambda_k \\ \Sigma^{-1}\mu_k \end{matrix} \right ]\end{split}\]

人为的给特定向量x在第一个位置增加一个常数元素1，然后用新的参数简化后验概率公式 公式(16.5.5) 后为：

(18.3.39)\[p(Y^k=1|x;\theta) = \frac{e^{\beta_k^T x}}{ \sum_{l=1}^{K} e^{\beta_l^T x}}\]

这个函数通常也被称为softmax函数，softmax函数是逻辑函数的扩展，逻辑函数是2分类函数，softmax扩展成多分类， softmax拥有和逻辑函数类似的几何解释。

图 18.3.7 softmax函数在特征空间上的轮廓线。图中的实直线表示两个类别概率相同 \(\phi_k(z)=\phi_l(z)\) 的位置， 类别 \(k\) 和类别 \(l\) 后验概率相同的轮廓线。

多分类高斯分类模型的最大似然估计和二分类模型没有本质区别，参数的最大似然估计等于经验分布，区别就是原来样本被分成两类， 现在样本被分成多类。

(18.3.40)\[ \begin{align}\begin{aligned}\hat{\lambda}_{k,ML} &= \frac{\sum_{n=1}^N \delta(y_n=y_k) }{N}\\\hat{\mu}_{jk,ML} &= \frac{\sum_{n=1}^N \delta(y_n=y_k) x_{j,n}}{\sum_{n=1}^N \delta(y_n=y_k)}\\ \hat{\sigma}^2_{j,ML} &= \sum_{k=1}^K \frac{\sum_{n=1}^N \delta(y_n=y_k) (x_{j,n}-\hat{\mu}_{jk,ML})^2}{\sum_{n=1}^N \delta(y_n=y_k) }\end{aligned}\end{align} \]

本节我们讨论的高斯判别模型是一个线性分类(linear classifier)器， 当然如果把不同类别的高斯分布的协方差矩阵设置成不同的参数，就可以得到非线性分类器， 有兴趣的读者可以自己推导一下。

18.3.2. 朴素贝叶斯模型

在高斯判别模型中我们假设特征变量 \(X_j\) 是连续变量，并且服从高斯分布， 现在我们讨论当特征变量 \(X_j\) 是离散变量的情景。 假设每个特征 \(X_j\) 是有 S个可能取值的离散变量，并且在给定类别 \(Y\) 时， 特征变量满足条件独立属性，这样的模型被称为 朴素贝叶斯模型(naive Bayes classifier) 。 本节我们讨论朴素贝叶斯模型，包括其后验概率的计算以及参数的最大似然估计。

大部分过程和上一节是相同的，无非就是条件概率 \(p(X_j|Y)\) 有高斯分布变成了离散分布。 我们直接从多分类说起，同样假设类别变量 \(Y\) 是一个多项式分布，共有K个类别标签， 其先验概率分布是：

(18.3.41)\[p(y;\lambda) = \prod_{k=1}^K \lambda_i^{\delta(y=y_k) }\]

其中 \(\delta(y,y_k)\) 是指示函数，当 \(y=y_k\) 成立的时候值为1，否则值为0。 \(\lambda_k\) 表示变量 \(Y\) 是第k个类别的概率。

特征变量 \(X_j\) 同样看做是多项式变量，不同类别时服从不同参数的多项式分布。 用下标 \(j\) 表示第 \(j\) 个特征变量，假设一共有 \(m\) 个特征，每个特征都有S个取值， \(X_j^s\) 表示第j个特征变量的第s个取值， 符号 \(k\) 表示 \(Y\) 的 第 \(k\) 个类别标签， 类别条件概率分布为：

(18.3.42)\[p(x_j|Y^k=1;\eta) =\prod_{s=1}^S \eta_{kjs}^{\delta(x_j=x_j^s)}\]

其中 \(\eta_{kjs}\triangleq p(x^s_j=1|Y^k=1;\eta)\) 表示在类别 \(Y^k\) 的条件下， 离散特征变量 \(X_j\) 取值为第 \(s\) 个值的概率。

由于所有特征变量是条件独立的，在类别 \(Y^k\) 的条件下，全部特征的条件联合概率可以写成：

(18.3.43)\[p(x_1,\dots,x_j,\dots,x_m|Y^k=1;\eta_k) = \prod_{j=1}^{m} p(x_j|Y^k=1;\eta_k) = \prod_{j=1}^{m} \prod_s \eta_{kjs}^{\delta(x_j=x_j^s)}\]

联合概率

朴素贝叶斯模型的联合概率可以写成：

(18.3.44)\[p(x,y;\theta) = p(y;\lambda) \prod_{j=1}^m p(x_j|y;\theta_j)\]

其中 \(x=[x_1,\dots,x_j,\dots,x_m]\) 表示所有特征的特征向量。

后验概率

朴素贝叶斯模型的后验概率可以写成：

(18.3.45)\[ \begin{align}\begin{aligned}p(Y^k=1|x;\eta) &= \frac{p(y;\lambda) \prod_{j=1}^m p(x_j|y;\eta) }{p(x)}\\&= \frac{\lambda_k \prod_{j=1}^{m} \prod_s \eta_{kjs}^{\delta(x_j=x_j^s)} } {\sum_{l} \lambda_l \prod_{j=1}^{m} \prod_s \eta_{ljs}^{\delta(x_j=x_j^s)} }\\&= \frac{ \exp \{ \log \lambda_i + \sum_{j=1}^{m} \sum_s {\delta(x_j=x_j^s)} \log \eta_{kjs} \} } { \sum_{l} \exp \{ \log \lambda_l + \sum_{j=1}^{m} \sum_s {\delta(x_j=x_j^s)} \log \eta_{ljs} \} }\end{aligned}\end{align} \]

上述公式中，下标 \(k\) 表示第 \(k\) 个分类标签，下标 \(j\) 表示第 \(j\) 个特征变量，下标 \(s\) 表示特征变量 \(x_j\) 的第s个取值。 \(\eta_{kjs}\) 表示在类别为 \(Y^k\) 的条件下， 第 \(j\) 个多项式特征变量 \(X_j\) 取值为 \(x_{js}\) 的概率为。

我们简化一下符号，把 \(x_j\) 看做一个S维的向量，其中元素值只能是0或者1，当 \(x_j = x_{js}\) 时， 第s个元素为1，其余为0，例如： \(x_j=[0_1,\dots,1_s,\dots,0_S]\) 。同理，\(\log \eta_{kj}\) 也看成是一个S维的向量， 如此公式中的 \(\sum_s \delta(x_j=x_j^s) \log \eta_{kjs}\) 就可以看成是向量 \(x_j\) 和向量 \(\eta_{kj}\) 的內积， 这样我们就把下标 \(s\) 简化掉。

(18.3.46)\[ p(Y^k=1|x;\eta) = \frac{ \exp \{ \log \lambda_k + \sum_{j=1}^{m} {x_j} \log \eta_{kj} \} } { \sum_{l} \exp \{ \log \lambda_l + \sum_{j=1}^{m} {x_j} \log \eta_{lj} \} }\]

再进一步，我们用符号 \(x=[1,x_1,x_j,x_m]\) 表示特征向量， 向量中第一元素1是我们人为加入的一个虚拟的常数值特征。 并且定义一个新的参数向量 \(\beta\) :

(18.3.47)\[\begin{split}\beta_k \triangleq \left [ \begin{matrix} \log \lambda_l \\ \log \eta_i \end{matrix} \right ]\end{split}\]

同样用內积的形式表示 \(\beta\) 和 \(x\) 的关系，最终我们得到了softmax的标准形式， 多分类朴素贝叶斯后验概率是一个特征线性组合的softmax函数：

(18.3.48)\[p(Y^k=1|x;\eta)=\frac{\exp \{\beta_k^Tx \} }{\sum_l \exp \{\beta_l^T x\} }\]

在二分类的时，可以在softmax函数上，分子分母同时除以分子，得到二分类的逻辑函数，逻辑函数可以做是softmax函数的简化版本。

(18.3.49)\[p(Y=1|x;\theta) = \frac{1}{1+\exp \{ -\theta^T x \}}\]

最大似然估计

最后我们讨论下朴素贝叶斯模型的最大似然估计，我们再次假设我们有N个观测样本组成的训练集 \(\mathcal{D}\) ， \(\mathcal{D}=\{(x_n,y_n);n=1,\dots,N \}\) 。

根据朴素贝叶斯模型的联合概率 公式(18.3.44) ，对数似然函数可以写成：

(18.3.50)\[\ell(\theta;\mathcal{D}) = \sum_{n=1}^N \log p(y_n;\lambda) + \sum_{n=1}^N \sum_{j=1}^m \log p(x_{j,n}|y_n;\eta)\]

对数似然函数解耦成两部分，其中第一部分可以独立进行最大化估计出参数 \(\lambda\) ， 这就是一个多项式分布的最大似然估计估计，我们可以直接给出最大似然估计估计的结果， 我们用符号 \(\mathcal{D}(y^k)\) 表示数据集中类别 \(y^k\) 的数量。

(18.3.51)\[\hat{\lambda_k} = \frac{\sum_{n=1}^N \delta(y_n,y^k) }{N} = \frac{\mathcal{D}(y^k)}{N}\]

现在我们来看第二项参数 \(\eta\) 的估计，我们把第二项进行展开，注意 \(n\) 是观测样本的编号， \(k\) 是类别的编号，\(j\) 是特征的编号，\(s\) 是特征的离散值编号。

(18.3.52)\[\sum_{n=1}^N \sum_{j=1}^m \log p(x_{j,n}|y_n;\eta) = \sum_{n=1}^N \sum_{k=1} \sum_{j} \sum_{s} \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) \log \eta_{kjs}\]

条件概率分布 \(p(x|y)\) 是一个多项式分布，我们在讨论多项式分布最大似然估计的章节中讲过，多项式分布的最大似然估计是一个带有约束的最优化问题， 需要引入一个拉格朗日因子 \(\lambda\) ，注意，这里符号有些冲突，这之后的符号 \(\lambda\) 表示拉格朗日因子， 不再是类别变量 \(Y\) 的边缘概率分布 \(p(y;\lambda)\) 中的参数。

(18.3.53)\[\tilde{\ell}(\eta;\mathcal{D}) \triangleq \sum_{n=1}^N \sum_{k} \sum_{j} \sum_{s} \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) \log \eta_{kjs} + \sum_{k} \sum_{j} \lambda_{kj} (1-\sum_s \eta_{kjs} )\]

求偏导：

(18.3.54)\[\frac{\partial \tilde{\ell} }{ \partial \eta_{kjs} } = \frac{ \sum_{n=1}^N \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) }{ \eta_{kjs}} - \lambda_{kj}\]

令其等于0，求解出 \(\eta_{kjs}\) :

(18.3.55)\[\eta_{kjs} = \frac{\sum_{n=1}^N \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) }{\lambda_{kj}}\]

又由于约束 \(\sum_s \eta_{kjs}=1\) ：

(18.3.56)\[ \begin{align}\begin{aligned}\sum_s \eta_{kjs} &= \sum_s \frac{ \sum_{n=1}^N \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) }{\lambda_{kj}}\\&= \frac{ \sum_{n=1}^N \sum_s \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) }{\lambda_{kj}}\\&= \frac{ \sum_{n=1}^N \delta(y_n, y^k) }{\lambda_{kj}} = 1\end{aligned}\end{align} \]

可得：

(18.3.57)\[\lambda_{ij} = \sum_{n=1}^N \delta(y_n, y^k)\]

再代回到偏导数中，并令偏导数为0，可以求得：

(18.3.58)\[\hat{\eta}_{kjs,ML} = \frac{ \sum_{n=1}^N \delta(x_{j,n},x_{j,n}^s) \delta(y_n, y^k) }{\sum_{n=1}^N \delta(y_n, y^k)}\]

其中，分母是类别 \(k\) 的样本总数，分子是在类别 \(k\) 的样本中，特征 \(x_j\) 取值为 \(x_j^{s}\) 的样本数量。 很明显，参数的估计值就是样本的经验统计值。

18.3.3. 指数族

至此，我们讨论的所有生成模型，其后验概率都会得到一个简单的函数形式-二分类的逻辑函数和多分类的softmax函数。 对于多项式和高斯类别条件密度(类别协方差矩阵相同)，特征空间中的等后验概率轮廓线都是超平面。 事实上，我们将会看到，类别条件概率并不是只有多项式和高斯分布，很有其它的条件概率分布都是这样的。

指数族是一个包含很多概率分布的分布族，包括多项式分布和高斯分布，以及其它一些经典的分布，比如泊松分布， gamma分布，狄利克雷分布等等。这里我们讨论使用指数族的标准形式作为类别条件分布会得到怎样的结果。

指数族分布的标准函数形式为：

(18.3.59)\[p(x;\eta) = \exp \{ \eta^T x -A(\eta) \} h(x)\]

其中 \(\eta\) 是参数向量。

现在我们考虑一个二分问题，其中类别条件概率分布我们用指数族标准形式。 在类别 \(Y=1\) 的条件下，指数族分布的参数用 \(\eta_1\) 表示， 在类别 \(Y=0\) 的条件下，指数族分布的参数用 \(\eta_0\) 表示。

(18.3.60)\[ \begin{align}\begin{aligned}p(Y=1|x;\eta) &= \frac{p(Y=1;\lambda)p(x|Y=1;\eta_1)} {p(Y=1;\lambda)p(x|Y=1;\eta_1)+ p(Y=0;\lambda)p(x|Y=0;\eta_0)}\\ &= \frac{\lambda \exp \{ \eta_1^Tx - A(\eta_1) \}h(x) } {\lambda \exp \{ \eta_1^Tx - A(\eta_1) \}h(x) + (1-\lambda) \exp \{ \eta_0^Tx - A(\eta_0) \}h(x)}\\ &= \frac{1} {1 + \exp \{ -(\eta_0-\eta_1)^T x -A(\eta_0) +A(\eta_1) - \log \frac{\lambda}{1- \lambda} \} }\end{aligned}\end{align} \]

我发现，后验概率最终的到的就是逻辑函数的形式。

类似的，对于多分类场景，后验概率为标准的 softmax 函数形式：

(18.3.61)\[ \begin{align}\begin{aligned}p(Y^k=1|x;\eta) &= \frac{p(Y^k=1;\lambda) p(x|Y^k=1;\eta_k) } {\sum_l p(Y^l=1;\lambda) p(x|Y^l=1;\eta_l)}\\&= \frac{\lambda_k \exp \{ \eta_k^Tx - A(\eta_k) \} h(x) } { \sum_l \lambda_l \exp \{ \eta_l^Tx - A(\eta_l) \} h(x) }\\&= \frac{\exp \{ \eta_k^T x - A(\eta_k) + log \lambda_k \} } {\sum_l \exp \{ \eta_l^T x - A(\eta_l) + log \lambda_l \} }\end{aligned}\end{align} \]

重要

生成模型是对类别边缘概率分布 \(p(Y)\) 和类别条件概率分布 \(p(X|Y)\) 进行建模，并根据贝叶斯定理得到后验概率分布 \(p(Y|X)\) 。 理论上类别条件概率分布 \(p(X|Y)\) 的选择，需要根据特征数据的分布选择合适的概率分布， 如果概率分布选择的不合适，模型的效果自然不好。 所以生成式模型效果的好坏，会受到类别条件概率分布 \(p(X|Y)\) 的选择，而类别条件概率分布的选择又依赖于特征数据的分布。 然而实际场景中，很难保证所有特征都服从同一个概率分布，更进一步，一个特征数据很多时候不符合任意标准的概率分布。 这就是生成模型的局限性，生成模的使用需要建立在很强的数据假设上。

当使用指数族分布作为条件概率 \(p(X|Y)\) 的概率密度时，得到的后验概率分布将是逻辑函数(二分类)或者softmax(多分类) 函数的形式。

18.4. 判别模型

我们已经讨论完分类问题中的生成模型，生成模型的核心是为类别条件概率 \(p(X|Y)\) 选择一个合适的概率分布， 然而实际应用场景中这是非常困难。但是我们发现不管类别条件概率 \(p(X|Y)\) 为指数族中任意一个分布， 其后验概率分布 \(p(Y|X)\) 就具有一样的形式(二分类是逻辑函数，多分类是softmax函数)， 这就给了我们一个启示，是不是可以忽略类别条件概率分布的具体形式，而直接用逻辑函数或者softmax函数为后验概率分布 \(p(Y|X)\) 建模，然后直接学习出逻辑函数或者softmax函数的参数，这就是判别模型。 判别模型就是直接用一个决策函数 \(D(x)\) 为条件概率 \(p(Y|X)\) 进行建模。

(18.4.13)\[p(y|x) = D(x)\]

本节我们开始讨论分类问题的判别模型，在判别式分类模型中，我们直接为后验概率 \(p(Y|X)\) 进行建模， 而忽略类别条件概率。 \(fg_32_15\) 是判别式模型的图形表示， 特征变量是类别变量的父结点，在这张图中，我们把特征向量看做是分开的独立结点， 但是这里我们并不假设特征变量是条件独立的，事实上，在判别模型中，我们不对边缘概率 \(p(x)\) 做任何假设。判别式模型的目标是直接对条件概率 \(p(y|x)\) 进行建模。

图 18.4.2 softmax函数在特征空间上的轮廓线。图中的实直线表示两个类别概率相同 \(\phi_k(z)=\phi_l(z)\) 的位置，

18.4.1. 逻辑回归

我们从二分类问题开始，我们已经知道，生成式二分类模型的后验概率分布是一个参数化的逻辑函数(又叫sigmod函数)。 条件概率 \(p(y|x)\) 是在特征向量 \(x\) 和参数向量 \(\beta\) 的线性组合 \(z=\beta^T x\) 的基础上， 加了一个逻辑函数。

(18.4.14)\[ \begin{align}\begin{aligned}p(y|x) &= \frac{1}{1+\exp \{ -z \} }\\&= \frac{1}{1+\exp \{ -\beta^T x \} }\end{aligned}\end{align} \]

我们可以直接用这个函数作为参数化的分类模型，其中 \(\beta\) 是模型的参数向量，我们可以从训练数据集中学习出参数 \(\beta\) ，然后就可以用这个逻辑函数的模型对新样本进行预测分类。 因为这个分类模型是一个逻辑函数，所以我们称之为逻辑回归(logistic regression)分类模型， 虽然名字有回归，但这个一个分类模型。

对于二分类问题，类别标签 \(Y\) 是一个伯努利随机变量， 对于每一个输入特征 \(x\) ，逻辑回归模型得到的是类别标签为1的概率。 注意这个概率 \(p(Y=1|x)\) 相当于类别标签 \(Y\) 的条件期望。

(18.4.15)\[E(y|x) = 1 \times p(Y=1|x) + 0 \times p(Y=0|x)=p(Y=1|x)\]

因此，这类似于回归问题，目标是建模在给定 \(X\) 时变量 \(Y\) 的条件期望。 在回归的问题场景中，变量 \(Y\) 是一个连续值变量，我们在条件期望 \(E(y|x)\) 的基础上加了一个高斯误差 \(\epsilon\) 。 然而，在二分类的问题场景中，变量 \(Y\) 是一个伯努利离散变量， 我们定义 \(\mu(x)\triangleq p(Y=1|x)\) ，并且改写伯努利分布为：

(18.4.16)\[p(y|x)=\mu(x)^y (1-\mu(x))^{1-y}\]

我们把原来伯努利分布的参数 \(\mu\) 改成一个关于特征 \(x\) 的函数 \(\mu(x)\) 。

(18.4.17)\[p(Y=1|x;\theta) = \mu(x) = \frac{1}{1+ e^{-z(x)} }\]

条件期望 \(\mu(x)\) 通过一个內积 \(z(x)\triangleq \theta^T x\) 对 \(x\) 依赖， 其中 \(\theta\) 是参数向量，內积通过一个逻辑函数转化成概率形式。

相对应生成式模型，在这里我们避免了对类别条件概率 \(p(X|Y)\) 的任何假设， 直接用一个简单的参数化形式为后验概率 \(p(Y|X)\) 进行建模， 这就使得判别式模型比生成式模型拥有更好的适配性，不需要依赖太强的假设。

逻辑函数的特性

逻辑函数有一些非常有意思的特性，这些特性有很大应用价值。 首先逻辑函数是可逆的，逻辑函数表示从 \(z\) 到 \(u\) 的一个映射：

(18.4.18)\[\mu=\frac{1}{1+e^{-z}}\]

也可以反过来，写成从 \(u\) 到 \(z\) 的一个映射：

(18.4.19)\[z = \log \left ( \frac{\mu}{1-\mu} \right )\]

这个函数也称为对数几率比(log odds)。

这种可逆的特性简化了求导：

(18.4.20)\[ \begin{align}\begin{aligned}\frac{dz}{d\mu} &= \frac{d}{d\mu} \log \left ( \frac{\mu}{1-\mu} \right )\\&= \frac{1}{\mu(1-\mu)}\\ \frac{d\mu}{dz} &= \mu(1-\mu)\end{aligned}\end{align} \]

似然估计

我们我们讨论如何通过最大似然估计得到逻辑回归模型的参数， 假设训练集样本为 \(\mathcal{D}=\{ (x_n,y_n);n=1,\dots,N \}\) ，其中任意一条样本的发生概率为：

(18.4.21)\[p(y_n|x_n;\theta) = \mu(x_n)^{y_n} (1-\mu(x_n))^{1-y_n}\]

其中 \(\mu(x_n)=1/(1+e^{-\theta^T x_n})\) 。 全部训练集样本的联合概率为：

(18.4.22)\[p(y_1,\dots,y_N|x_1,\dots,x_N;\theta)=\prod_{n} \mu(x_n)^{y_n} (1-\mu(x_n))^{1-y_n}\]

对数似然函数为：

(18.4.23)\[\ell(\theta|\mathcal{D}) = \sum_{n} \{ y_n \log \mu(x_n) + (1-y_n)\log(1-\mu(x_n)) \}\]

我们通过最大化对数似然函数的方式求解参数向量 \(\theta\) ， 对数似然函数的导数为：

(18.4.24)\[ \begin{align}\begin{aligned}\nabla_{\theta} \ell &= \sum_n \left ( \frac{y_n}{\mu(x_n)} - \frac{1-y_n}{1-\mu(x_n)} \right ) \frac{d \mu(x_n)}{d z(x_n)} \frac{d z(x_n)}{d \theta}\\&= \sum_n \frac{y_n-\mu(x_n)}{\mu(x_n)(1-\mu(x_n))} \mu(x_n)(1-\mu(x_n)) x_n\\&= \sum_n (y_n-\mu(x_n)) x_n\end{aligned}\end{align} \]

有意思的是我们发现这个偏导数和线性回归模型的似然的偏导数是一样的， 同理，这里我们也无法直接求得解析解，而是需要使用迭代法求解。 类似的，这里我们也介绍两种迭代算法，一个是在线学习算法，一个是批量学习算法。

在线学习算法

迭代重加权最小二乘法

离散特征做 one-hot

18.4.1.1. 几率比(odds)

OR值（odds ratio）又称比值比、优势比

odds 可以用来判断特征的重要性，或者说相关性？

参考 Generalized Linear Models and Extensions-Stata Press (2018) 9.4 节

https://rstudio-pubs-static.s3.amazonaws.com/182726_aef0a3092d4240f3830c2a7a9546916a.html

https://www.statisticssolutions.com/theres-nothing-odd-about-the-odds-ratio-interpreting-binary-logistic-regression/

https://www.theanalysisfactor.com/why-use-odds-ratios/

(18.4.25)\[logit(p)= log(\frac{p}{1-p})=\beta_{0}+\beta_{1} x_{1}+...+\beta_{x} x_{x}\]

(18.4.26)\[odds = \frac{p}{1-p} = e^{z}\]

18.4.2. 多分类

本节我们讨论逻辑回归模型的一般化扩展，多分类问题的判别模型。 回顾一下生成模型， 当类别条件概率 \(p(X|Y)\) 是指数族分布时， 后验条件概率 \(p(Y|X)\) 具有线性softmax函数形式。

(18.4.27)\[p(Y^k=1|x;\theta) = \frac{\exp \{ \theta_k^Tx\} }{\sum_l \exp \{ \theta_l^T x \} }\]

判别式模型就是直接学习这个线性softmax函数的参数，然后直接使用其对新样本进行分类预测。 换句话说，就是用这个softmax函数作为条件概率 \(p(Y|X)\) 的概率质量函数， 而不再是像生成模型那样利用贝叶斯定理求得，这就是判别式和生成式的本质区别。 判别式模型的优点是不再需要对类别条件概率 \(p(X|Y)\) 进行建模， 也就是说我们不需要关注 \(p(X|Y)\) 到底是服从什么分布，不需要对齐进行很强的分布假设， 只要其是指数族分布中一种，其后验概率 \(p(X|Y)\) 都具有线性softmax函数的形式。 我们把softmax多分类的判别式模型称为 softmax 回归(softmax regression) ，这个命名是和 逻辑回归(logistic regression) 对应的。

softmax 函数的特性

softmax函数用于一些和logistic函数类似的特性。 我们用符号 \(\mu^k\) 表示样本属于第 \(k\) 个类别的概率， 用符号 \(\eta_n^k=\theta_k^T x_n\) 表示线性softmax函数中的线性组合部分。 我们把 \(\mu\) 和 \(\eta\) 都看作是向量变量，上标表示向量的第几个元素。 \(\mu^k\) 表示向量 \(\mu\) 的第 \(k\) 个元素， \(\eta^k\) 表示向量 \(\eta\) 的第 \(k\) 个元素。 softmax函数可以改写成向量 \(\eta\) 到向量 \(\mu\) 的一个映射。

(18.4.28)\[\mu^k = p(Y^k=1|x;\theta) = \frac{\exp \{\eta^k \} }{\sum_l \exp \{ \eta^l \} }\]

这个函数是可逆的，等号两边都添加一个对数

(18.4.29)\[ \begin{align}\begin{aligned}\log \mu^k &= \log \exp \{\eta^k \} - \log {\sum_l \exp \{ \eta^l \} }\\ \eta^k &= \log \mu^k + \log {\sum_l \exp \{ \eta^l \} }\end{aligned}\end{align} \]

其中 \(\log {\sum_l \exp \{ \eta^l \} }\) 是一个常数。

现在来看一下softmax函数的偏导数。注意，softmax函数比较特殊，其分母部分是一个基于类别k的求和， 包含了所有的类别k，所以softmax函数其实是一个向量函数。向量函数求偏导是对于每个元素都要求的，得到的是一个偏导数矩阵， 俗称 雅可比矩阵(Jacobi) ， 不熟悉的读者可以自行查看相关资料。 softmax函数输出值 \(\mu\) 对参数 \(\eta\) 的偏导，需要求任意的 \(\mu_i\) 对任意的 \(\eta_j\) 的偏导，这里可以分为 \(i=j\) 和 \(i \ne j\) 两种情况讨论。

当 \(i=j\) 时：

(18.4.30)\[ \begin{align}\begin{aligned}\frac{\partial \mu^i}{\partial \eta^j} &= \frac{\partial \mu^i}{\partial \eta^i}\\&= \frac{ (\sum_k e^{\eta^k} ) e^{\eta^i} - e^{\eta^i}e^{\eta^i} }{(\sum_k e^{\eta^k})^2}\\&= \mu_i(1-\mu_i)\end{aligned}\end{align} \]

当 \(i \ne j\) 时：

(18.4.31)\[ \begin{align}\begin{aligned}\frac{\partial \mu^i}{\partial \eta^j} &= \frac{ - e^{\eta^i}e^{\eta^j} }{(\sum_k e^{\eta^k})^2}\\&= -\mu_i \mu_j\end{aligned}\end{align} \]

可以通过添加一个指示函数把两部分合并， 定义 \(\delta(i,j)\) 是指示函数，当 \(i=j\) 时，\(\delta(i,j)=1\) ， 当 \(i\ne j\) 时，\(\delta(i,j)=0\) 。

(18.4.32)\[ \begin{align}\begin{aligned}\frac{\partial \mu^i}{\partial \eta^j} &= \frac{ (\sum_k e^{\eta^k} ) e^{\eta^i} \delta(i,j) - e^{\eta^i}e^{\eta^j} }{(\sum_k e^{\eta^k})^2}\\&= \frac{e^{\eta^i}}{\sum_k e^{\eta^k}} \left ( \delta(i,j) - \frac{e^{\eta^j}}{\sum_k e^{\eta^k}} \right )\\&= \mu^i(\delta(i,j) - \mu^j)\end{aligned}\end{align} \]

最大似然估计

在多分类问题中输出变量 \(Y\) 是一个多项式随机变量， 我们用符号 \(\mu_n^k\) 表示第 \(n\) 条样本属于第 \(k\) 个类别的概率， 多项式分布可以写成如下的形式：

(18.4.33)\[p(y_n|x_n;\theta) = \prod_k \left ( \mu_n^k \right )^{\delta(y_n,k)}\]

其中 \(\delta(y_n,k)\) 是指示函数，当第 \(n\) 条样本的类别标签 \(y_n=k\) 时，函数输出1，否则输出0。 \(\theta=(\mu^1,\mu^2,\dots,\mu^K)^T\) 是多项式的参数向量。 对数似然函数为：

(18.4.34)\[ \begin{align}\begin{aligned}\ell(\theta;\mathcal{D}) &=\log \prod_n \prod_k \left ( \mu_n^k \right )^{\delta(y_n,k)}\\&= \sum_n \sum_k {\delta(y_n,k)} \log \left ( \mu_n^k \right )\\&= \sum_n \sum_k {\delta(y_n,k)} \log \left ( \frac{\exp \{\eta^k_n \} }{\sum_l \exp \{ \eta^l_n \} } \right )\\&= \sum_n \sum_k {\delta(y_n,k)} \log \left ( \frac{\exp \{\theta_k^T x_n \} }{\sum_l \exp \{ \theta_l^T x_n \} } \right )\end{aligned}\end{align} \]

现在我们需要计算这个对数似然函数关于参数 \(\theta_i\) 的梯度(偏导数)， 注意 \(\theta_i\) 是一个向量，表示第 \(i\) 个类别的参数向量。

(18.4.35)\[ \begin{align}\begin{aligned}\nabla_{\theta_i} \ell &= \sum_n \sum_k \frac{\partial \ell}{\partial \mu_n^k} \frac{\partial \mu_n^k}{\partial \eta_n^i} \frac{d \eta_n^i}{d \theta_i}\\&= \sum_n \sum_k \frac{\delta(y_n,k)}{\mu_n^k} \mu_n^k (\delta(i,k) - \mu_n^i) x_n\\&= \sum_n \sum_k \delta(y_n,k) (\delta(i,k) - \mu_n^i) x_n\\&= \sum_n ( \delta(y_n,i) - \mu_n^i) x_n\end{aligned}\end{align} \]

推导过程中我们利用了 \(\sum_k \delta(y_n,k)=1\) 的约束条件。 我们计算出的梯度形式上和逻辑回归、线性回归是一样的，这并不是一个巧合， 其反映了指数族概率分布的一般特性，在后续的广义线性模型章节我们会详细讨论。

就像逻辑回归和线性回归的一样，有了梯度之后可以通过在线参数学习法或者批量学习法学习参数， 在广义线性模型的章节我们会讨论适用于广义线性模型家族的一般形式的IRLS算法， 包括softmax回归和logistic回归。

18.4.3. 最大熵模型

18.4.4. Probit 回归

在讨论生成模型时，我们发现多种类型的类别条件概率(class-conditional)的后验概率都具逻辑函数的形式， 因此我们直接用逻辑函数对后验概率 \(p(Y|X)\) 进行建模，这种直接对后验条件概率进行建模的方法称之为判别模型。 本节我们介绍一种后验概率不是逻辑函数的判别模型，称为 Probit regression。 在probit模型中，继续采用线性假设，即未知参数和输入变量 \(X\) 是线性组合 \(\theta^Tx\) ， 只是把线性组合部分转化成概率形式的”转换函数”不再是logistic函数。

18.4.5. Noisy-OR 模型

18.4.6. 其它指数模型