18.1. 负二项式分布回顾指数族的各种分布,可以发现很多分布都和伯努利分布有关,二项式分布描述的是 \(n\) 次伯努利实验成功次数的概率分布,
而泊松分布又是二项式分布的极限形式,描述的是单位时间窗口内事件发生次数的概率分布。
指数分布又可以从泊松分布推导而来,描述的是下一次事件发生需要等待的时间。
指数分布的更一般化就得到了 Gamma
负二项式分布可以有多种定义(理解)方式,
有两种可以看做是二项式分布变种,另一种是可以看做是泊松-伽马混合模型。
关于负二项分布的”负”有多种解释,
最直观的一种就是,二项式分布描述的”成功”的次数,而负二项分布描述的是”失败”的次数,
因此是”负”。
18.1.1. 从二项式分布推导二项式分布表示的时进行 \(n\) 次伯努利实验 成功的次数 的概率分布,其概率分布函数为
(18.1.1) \[f(y;n,\pi) =\binom{n}{y} \pi^y(1-\pi)^{n-y}\]
其中 \(\pi\) 是单次伯努利实验成功的概率,
\(1-\pi\) 是伯努利实验失败的概率。符号 \(\binom{n}{y}\) 是组合数 \(C_{n}^y\) ,
表示 \(n\) 次实验中有任意 \(y\) 次成功的全部组合数。
二项式分布的期望和方差分别是
\(\mathbb{E}[Y]=n\pi\) 和 \(V(Y) = n \pi(1-\pi)\) 。
负二项式分布可以看做是二项式分布的变种,
并且有两种定义方式,事实上这两种定义方式是等价的。
首先回顾一些组合数计算的转换公式,其一有,
(18.1.2) \[C_{a+b}^a=C_{a+b}^b\]
其二,组合数的计算可以转换成多个 Gamma Gamma \(\Gamma(n+1)=n!\) ,
因此有
(18.1.3) \[C_n^k = \binom{n}{k} = \frac{n!}{k!(n-k)!}
= \frac{\Gamma(n+1) }{\Gamma(k+1)\Gamma(n-k+1)}\]
第一种定义方式
随机变量 \(Y\) 表示,伯努利实验中要得到成功 \(r\) 次的结果,需要进行的实验总次数,
\(r\) 必须是一个正整数。注意,一共进行了 \(y\) 次实验,最后一次实验一定是成功的,并且是第 \(r\) 次成功。
因此只需要在前面 \(y-1\) 次实验中任意成功 \(r-1\) 次即可,这符合二项式分布的定义,
根据二项式分布的概率分布函数 公式(18.1.1) 可以得到 \(y-1\) 次实验中成功 \(r-1\) 的概率为
\(Bin(y-1,r-1)\) ,第 \(y\) 次是成功的,其概率是 \(\pi\)
,因此实验总次数的变量 \(Y\) 的概率分布函数为
(18.1.4) \[ \begin{align}\begin{aligned}f(y;r,\pi) & = \underbrace{Bin(y-1,r-1)}_{\text{前(y-1)次}} \times
\underbrace{\pi}_{\text{第y次}}\\&= \binom{y-1}{r-1} \pi^{r-1}(1-\pi)^{y-r} \pi\\&= \binom{y-1}{r-1} \pi^{r}(1-\pi)^{y-r}\\&= \frac{\Gamma(y)}{\Gamma(r)\Gamma(y-r-1) } \pi^{r}(1-\pi)^{y-r}\end{aligned}\end{align} \]
第二种定义方式
变量 \(Y\) 表示事件第 \(r\) 次成功前失败的次数。
注意是一共成功了 \(r\) 次,在这之前失败了 \(y\) 次,实验总次数是 \(y+r\) 。
由于第 \(y+r\) 次一定是成功的,故只要在前面的 \(y+r-1\) 次中找出成功的 \(r-1\)
次的组合次数即可,这符合二项式分布 \(Bin(y+r-1,r-1)\) ,
最终变量 \(Y\) 的概率分布为
(18.1.5) \[ \begin{align}\begin{aligned}f(y;r,\pi) &= \underbrace{ Bin(y+r-1,r-1) }_{\text{前(y+r-1)次}} \times
\underbrace{\pi}_{\text{第(y+r)次}}\\&=\binom{y+r-1}{r-1} \pi^{r-1} (1-\pi)^{y} \pi\\&=\binom{y+r-1}{r-1} \pi^{r} (1-\pi)^{y}\\&=\binom{y+r-1}{y} \pi^{r} (1-\pi)^{y}\\&= \frac{\Gamma(y+r) }{\Gamma(y+1)\Gamma(r)} \pi^{r}(1-\pi)^{y}\end{aligned}\end{align} \]
无论哪种方式,\(r\) 的含义都是一样的,
公式(18.1.5) 是 公式(18.1.4) 的平移,相当于把 \(y\)
平移到 \(y+r\) ,二者的概率分布曲线是完全一致的,
只是对变量 \(Y\) 的定义有些差异,但这不影响使用,
二者可以看做是等价的。
18.1.2. 泊松-伽马混合分布假设变量 \(Y\) 是泊松变量,其概率质量函数为
(18.1.6) \[P(Y) = \frac{\lambda^y e^{-\lambda}} {y!}\]
其中唯一的参数 \(\lambda\) 是泊松分布的期望参数,
在本书之前的所有内容中,都是假设概率分布的参数是数值参数,不是随机量。
现在我们假设泊松分布的期望参数 \(\lambda\) 也是一个随机量,
并且它的概率分布是 Gamma Gamma 公式(16.2.11)
的参数化方法,两个参数分别是形状(shape)参数 \(\alpha\) 和尺度(scale)参数 \(\beta\) 。
(18.1.7) \[f(\lambda;\alpha,\beta) =
\frac{ \beta^{\alpha} }{ \Gamma(\alpha)} \lambda^{\alpha-1} e^{-\beta \lambda }
\quad (\lambda,\alpha,\beta > 0)\]
此时响应变量 \(Y\) 和参数变量 \(\lambda\) 的联合概率分布为
\(p(Y,\lambda)=p(\lambda) p(Y|\lambda)\) ,
需要通过边缘化(积分消掉参数变量)的方法得到边缘概率 \(p(Y)\) 。
(18.1.8) \[P(Y) = \int_0^{\infty} P(\lambda) P(Y|\lambda) d \lambda\]
把 公式(18.1.6) 和 公式(18.1.7) 代入到 公式(18.1.8)
,并计算积分得到变量 \(Y\) 边缘概率分布函数。
(18.1.9) \[ \begin{align}\begin{aligned}f(y) &= \int_0^{\infty}
\frac{ \beta^{\alpha} \lambda^{\alpha-1} e^{-\beta \lambda } }{ \Gamma(\alpha)}
\frac{\lambda^y e^{-\lambda}} {y!} d \lambda\\&= \int_0^{\infty} \frac{ \beta^{\alpha} }{ \Gamma(\alpha) y!}
\lambda^{\alpha-1} e^{- \beta \lambda } \lambda^y e^{-\lambda} d \lambda\\&= \int_0^{\infty} \frac{ \beta^{\alpha} }{ \Gamma(\alpha) y!}
\lambda^{\alpha+y-1} e^{- (\beta+1) \lambda } d \lambda\\&= \frac{ \beta^{\alpha} }{ \Gamma(\alpha) y!} \int_0^{\infty}
\lambda^{\alpha+y-1} e^{- (\beta+1) \lambda } d \lambda\\&= \frac{ \beta^{\alpha} }{ \Gamma(\alpha) y!}
\int_0^{\infty}
\frac{ \Gamma(\alpha+y)}{ (\beta+1)^{\alpha+y} }
\frac{ (\beta+1)^{\alpha+y} }{ \Gamma(\alpha+y)}
\lambda^{\alpha+y-1} e^{- (\beta+1) \lambda } d \lambda\\&= \frac{ \beta^{\alpha} }{ \Gamma(\alpha) y!}
\frac{ \Gamma(\alpha+y)}{ (\beta+1)^{\alpha+y} }
\underbrace{\int_0^{\infty}
\underbrace{ \frac{ (\beta+1)^{\alpha+y} }{ \Gamma(\alpha+y)}
\lambda^{\alpha+y-1} e^{- (\beta+1) \lambda } }_{ Gamma(\alpha+y,\beta+1) } d \lambda }_{\text{积分为1}}\\&= \frac{ \beta^{\alpha} }{ \Gamma(\alpha) y!}
\frac{ \Gamma(\alpha+y)}{ (\beta+1)^{\alpha+y} }\\&= \frac{\Gamma(y+\alpha) }{\Gamma(y+1) \Gamma(\alpha) }
\frac{\beta^{\alpha}}{(\beta+1)^{\alpha} (\beta+1)^{y} }\\&= \frac{\Gamma(y+\alpha) }{\Gamma(y+1) \Gamma(\alpha) }
\left ( \frac{\beta}{\beta+1} \right )^{\alpha}
\left ( \frac{1}{\beta+1} \right )^{y}\end{aligned}\end{align} \]
现在重新参数化 公式(18.1.9) ,令 \(r=\alpha,\pi=\beta/(\beta+1)\)
,则公式 公式(18.1.9) 可以转化成
(18.1.10) \[f(y;r,\pi) =\frac{\Gamma(y+r) }{\Gamma(y+1) \Gamma(r) }
\pi^r (1-\pi)^y\]
这和 公式(18.1.5) 完全一样的,可见泊松-伽马混合模型本质上就是负二项式分布。
18.1.3. 辅助参数 \(\alpha\) 的影响负二项式分布有两个参数,一个是期望参数 \(\mu\) ,
一个是辅助参数 \(\alpha\) ,
根据前面的推导过程可知辅助参数 \(\alpha\) 一定是大于0的,
首先给 \(\alpha\) 赋值一个接近 \(0\) 的值,
观察下当 \(\alpha \approx 0\) 时负二项式分布的特点。
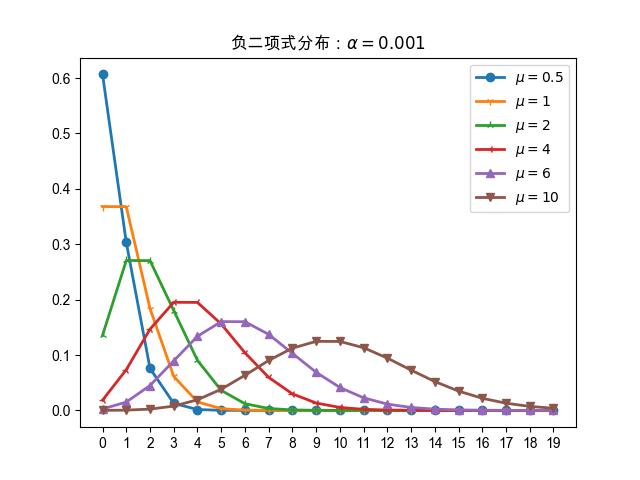
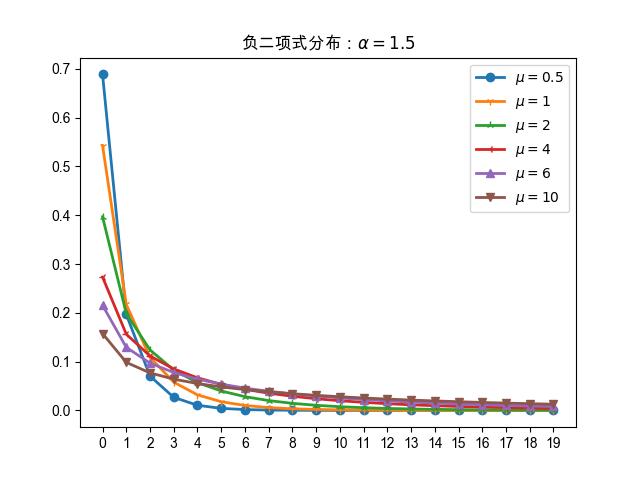
图 18.1.1 \(\alpha=0.001\) 时
负二项式分布概率质量函数的曲线图。
备注
注意,负二项式分布是离散变量的的分布,离散分布的概率分布函数称为概率质量函数,
概率质量函数应该是离散的点图,为了方便观测概率的变化规律,
我们把点图用线连接起来,观察曲线的变化。
图 18.1.1 当 \(\alpha=0.001\) 时,不同 \(\mu\) 值下负二项式分布的概率质量函数
对比下 图 18.1.1 图 14.1.1 \(\alpha=0\) 时,就等价于泊松分布,
泊松分布可以看做是负二项式分布的一个特例 。
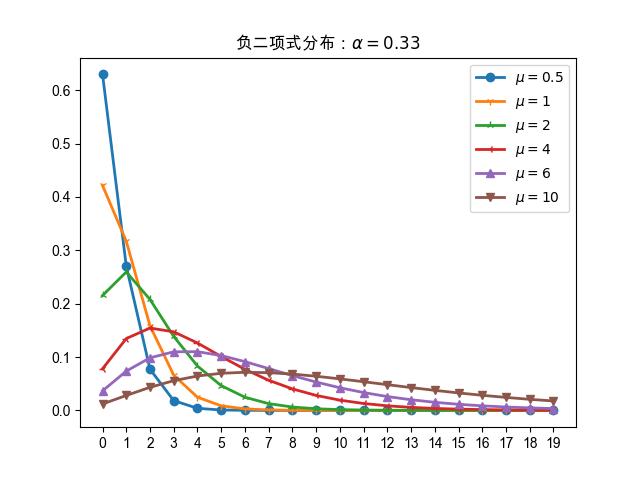
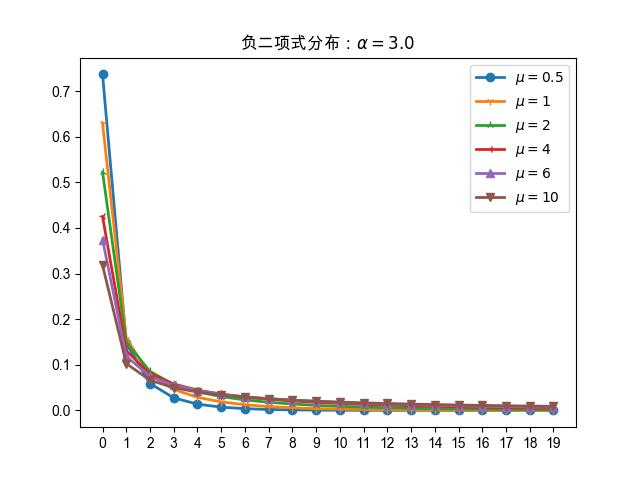
图 18.1.2 当 \(\alpha=0.33\) 时,不同 \(\mu\) 值下负二项式分布的概率质量函数。
相比于 \(\alpha=0.001\) 时,曲线凸起的部分向左移动了。
现在我们逐渐增大 \(\alpha\) 的值,
图 18.1.2 \(\alpha=0.33\) 的分布图,
可以看出曲线上凸起的部分向左移动了一些。
我们继续增大 \(\alpha\) 的值,
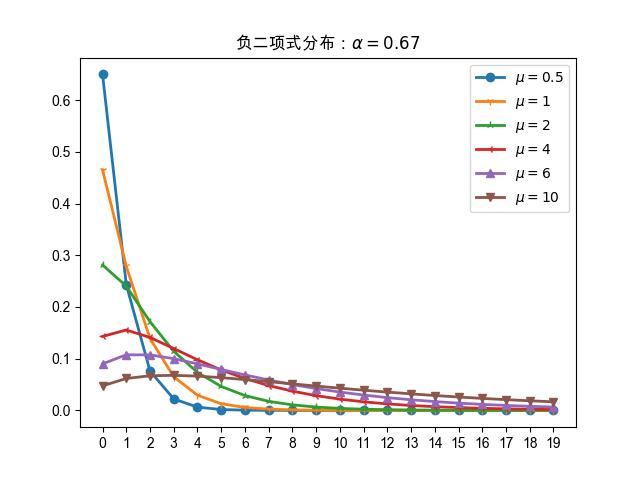
如 图 18.1.3 \(\alpha\) 设置为 \(0.67\) ,
可以发现原来凸起的部分逐渐消失。
图 18.1.3 当 \(\alpha=0.67\) 时,图形左侧凸起逐渐消失了。
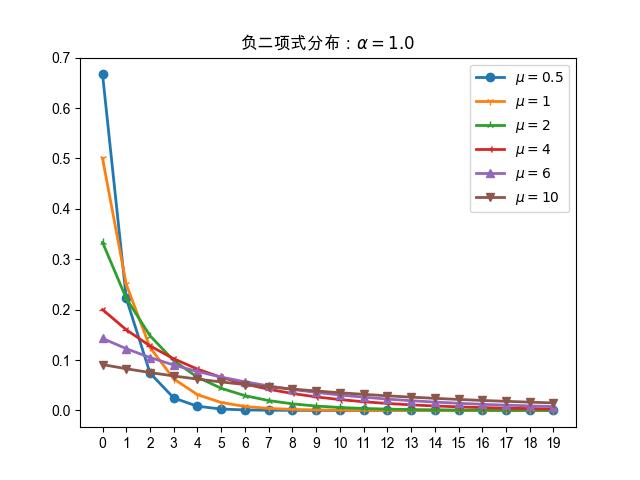
把 \(\alpha\) 的值进一步增大到 \(1.0\) ,
变成了 图 18.1.3 \(\alpha=1.0\) 的负二项式分布又叫做几何(geometric)分布,
几何分布是负二项式分布的一个特例 。
对比下 图 18.1.4 图 15.1.1 事实上几何分布是指数分布的离散版本,指数分布是一个连续值概率分布,而几何分布与指数分布是离散相关的 。
备注
指数分布是连续值概率分布,连续值随机变量的概率分布函数叫做概率密度函数(probability density function,pdf);
离散随机变量的概率分布函数叫做概率质量函数(probability mass function,pmf)。
概率密度函数的曲线图纵坐标不是概率值,需要积分才能得到概率值;
而概率质量函数的曲线图纵坐标直接就是对应的概率值。
图 18.1.4 当 \(\alpha=1.0\) 时,负二项式分布又称为几何分布,并且和指数分布是离散相关的。
继续增大 \(\alpha\) 的值,如 图 18.1.5 图 18.1.6 \(\alpha\) 的增加,各个不同的期望 \(\mu\) 值的曲线会逐渐重合在一起,
这意味着当 \(\alpha\) 足够大时,期望参数 \(\mu\) 的影响力逐渐变小。
图 18.1.5 当 \(\alpha=1.0\) 时,不同 \(\mu\) 值下负二项式分布的概率质量函数
图 18.1.6 当 \(\alpha=1.0\) 时,不同 \(\mu\) 值下负二项式分布的概率质量函数
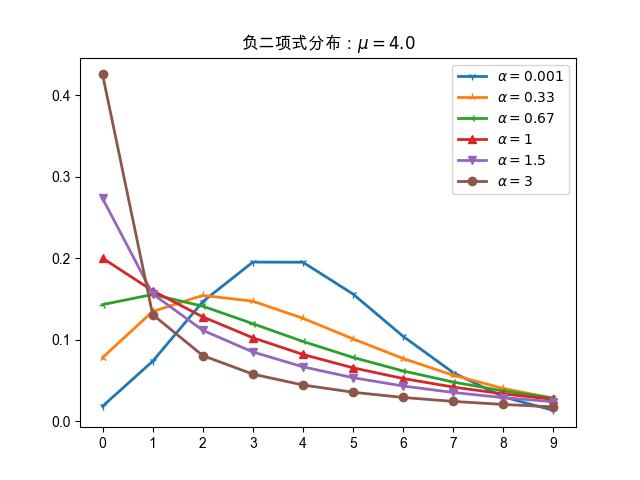
最后我们固定 \(\mu\) 的值,直接对比不同的 \(\alpha\) 下图形的差异。
图 18.1.7 \(\mu\) 固定为 \(4.0\)
,\(\alpha\) 取不同值时负二项式分布的图形。
可以看出,\(\alpha\) 等于 \(0\) 时,
负二项式分布在期望值附近的概率时最大的,
而随着 \(\alpha\) 增大,负二项式分布中 \(0\) 的概率逐步增大。
图 18.1.7 固定 \(\mu=4.0\) ,不同 \(\alpha\) 的值对图形的影响。
反过来,
固定 \(\alpha\) 的值,\(\mu\) 越大,\(0\) 的概率就越小,图形就越接近高斯分布。
最后我们总结下负二项式分布中 \(\mu\) 和 \(\alpha\) 的关系。
18.2. 负二项回归模型负二项式分布同样属于指数族分布,因此负二项式回归模型可以纳入到GLM框架中,
作为GLM的一员。
先把 公式(18.1.10) 作为负二项式分布的概率分布函数,并把它转化成指数族的形式。
(18.2.1) \[ \begin{align}\begin{aligned}f(y;r,\pi) &= \exp \left \{ \ln \left [ \frac{\Gamma(y+r) }{\Gamma(y+1) \Gamma(r) }
\pi^r (1-\pi)^y \right ] \right \}\\&= \exp \left \{
y \ln (1-\pi) + r\ln \pi + \ln \frac{\Gamma(y+r) }{\Gamma(y+1) \Gamma(r) }
\right \}\end{aligned}\end{align} \]
因此,有
(18.2.2) \[ \begin{align}\begin{aligned}\text{自然参数} & \quad \theta = \ln (1-\pi)\\& \quad \pi = 1- e^\theta\\\text{累积分布函数} & \quad b(\theta) = - r\ln \pi = -r \ln (1-e^\theta)\\\text{分散函数} & \quad a(\phi) = 1\end{aligned}\end{align} \]
现在来看下负二项式分布的期望与方差,指数族分布的期望与方差函数可以分别由
累积分布函数 \(b(\theta)\) 的一阶导和二阶导得到。
(18.2.3) \[ \begin{align}\begin{aligned}b'(\theta) &= \frac{\partial b}{ \partial \pi} \frac{\partial \pi}{ \partial \theta}\\&= \left (- \frac{r}{\pi} \right ) \{ -(1-\pi) \}\\&= \frac{r(1-\pi)}{\pi}\\&= \mu\end{aligned}\end{align} \]
(18.2.4) \[ \begin{align}\begin{aligned}b''(\theta) &= \frac{\partial^2 b}{ \partial \pi^2} \left (\frac{\partial \pi}{ \partial \theta} \right )^2
+ \frac{\partial b}{ \partial \pi} \frac{\partial^2 \pi}{ \partial \theta^2}\\&= \left ( \frac{r}{\pi^2} \right )(1-\pi)^2 + \frac{r}{\pi}(1-\pi)\\&=\frac{r(1-\pi)^2 +r\pi(1-\pi) }{\pi^2}\\&= \frac{r(1-\pi)}{\pi^2}\\&= \mu + \frac{\mu^2}{r}\\&= \nu(\mu)\end{aligned}\end{align} \]
有了方差函数后,可得到方差为
(18.2.5) \[V(Y) = a(\phi)\nu(\mu) = \mu + \frac{\mu^2}{r}\]
这个形式下的方差函数,参数 \(r\) 在分母的位置,不是很”美观”,
通常情况下会重新参数化一下,令 \(\alpha=1/r\)
,使用参数 \(\alpha\) 重新参数化负二项式模型后,负二项式分布的期望和方差分别为
(18.2.6) \[ \begin{align}\begin{aligned}\text{期望} & \quad \mu = \frac{1-\pi}{\alpha \pi}\\ & \quad \pi = \frac{1}{1+\alpha \mu}\\\text{方差} & \quad V(Y) = \mu + \alpha \mu^2\end{aligned}\end{align} \]
负二项式分布的概率分布函数 公式(18.2.1) 用期望参数 \(\mu\) 和 参数 \(\alpha\)
重新参数化后为
(18.2.7) \[ \begin{align}\begin{aligned}f(y;\alpha,\mu) &= \exp \left \{
y \ln (1-\pi) + r\ln \pi + \ln \frac{\Gamma(y+r) }{\Gamma(y+1) \Gamma(r) }
\right \}\\&= \exp \left \{
y \ln \left (\frac{\alpha \mu}{1+\alpha \mu} \right )- \frac{1}{\alpha} \ln (1+\alpha \mu) + \ln \frac{\Gamma(y+1/\alpha) }{\Gamma(y+1) \Gamma(1/\alpha) }
\right \}\end{aligned}\end{align} \]
公式(18.2.7) 是负二项式模型的标准指数族形式,其标准连接函数为
(18.2.8) \[\eta = \theta = \ln \left (\frac{\alpha \mu}{1+\alpha \mu} \right )\]
标准连接函数的响应函数为
(18.2.9) \[\mu = \frac{\exp(\eta)}{\alpha[1-\exp(\eta)] }\]
采用标准连接函数的负二项式模型通常简称为 NB-C
因此有
(18.2.10) \[ \begin{align}\begin{aligned}\text{自然参数} & \quad \theta = \ln \left (\frac{\alpha \mu}{1+\alpha \mu} \right )\\
\text{累积分布函数} & \quad b(\theta) = \frac{1}{\alpha} \ln (1+\alpha \mu)\\\text{期望} & \quad b'(\theta) = \mu\\\text{方差函数} & \quad \nu(\mu) = b''(\theta) = \mu + \alpha \mu^2\\\text{分散函数} & \quad a(\phi) = 1\\\text{方差} & \quad V(Y) = a(\phi)\nu(\mu) = \mu + \alpha \mu^2\\\text{标准连接函数} & \quad g(\mu) = \ln \left (\frac{\alpha \mu}{1+\alpha \mu} \right )\\\text{标准连接函数一阶导} & \quad g'(\mu) = \frac{1}{\mu+\alpha \mu^2}\\\text{响应函数} & \quad \mu = \frac{\exp(\eta)}{\alpha[1-\exp(\eta)] }\end{aligned}\end{align} \]
18.3. 参数估计参数 \(\alpha\) 通常被称为辅助(ancillary)参数或者尺度(scale)参数
,
只有 \(\alpha\) 是一个常数的时,负二项式回归模型才能纳入到 GLM GLM IRLS \(\beta\) ,
无法同时估计出额外的参数,需要在应用 IRLS \(\alpha\) 的值,然后把 \(\alpha\) 的值代入到GLM中,当做一个常量值。
我们先给出 NB-C IRLS \(\alpha\)
和协变量参数 \(\beta\)
。
18.3.1. IRLSNB-C 公式(18.2.7)
,其对数似然函数为
(18.3.1) \[\ell(\mu;y,\alpha) = \sum_{i=1}^N \left \{
y_i \ln \left (\frac{\alpha \mu_i}{1+\alpha \mu_i} \right )
- \frac{1}{\alpha} \ln (1+\alpha \mu_i)
+ \ln \Gamma(y_i+1/\alpha)
- \ln \Gamma(y_i+1) - \ln \Gamma(1/\alpha)
\right \}\]
NB-C
(18.3.2) \[g(\mu) = \ln \left (\frac{\alpha \mu}{1+\alpha \mu} \right )
= - \ln [ 1+ 1/ (\alpha \mu ) ]\]
标准连接函数的导数为
(18.3.3) \[g'(\mu) = \frac{1}{\mu+\alpha \mu^2}\]
依此可以给出 IRLS \(W\) 和工作响应矩阵 \(Z\)
,分别为
(18.3.4) \[ \begin{align}\begin{aligned}W_{ii} &= \frac{ 1}{ a(\phi) \nu(\hat{\mu}_i) ( g' )^2}\\&=
\hat{\mu}_i + \alpha \hat{\mu}_i^2\end{aligned}\end{align} \]
(18.3.5) \[ \begin{align}\begin{aligned}Z_i &= (y_i- \hat{\mu}_i) g' + \eta_i\\ &= \frac{(y_i- \hat{\mu}_i)}{\hat{\mu}_i + \alpha \hat{\mu}_i^2} + \eta_i\end{aligned}\end{align} \]
偏差统计量为
(18.3.6) \[D = 2\sum_{i=1}^N \left \{
y_i \ln \left ( \frac{y_i}{ \hat{\mu}_i} \right )
- \left ( y_i + \frac{1}{\alpha} \right ) \ln \left ( \frac{1+\alpha y_i}{1+\alpha \hat{\mu}_i} \right )
\right \}\]
NB-C
\(\mu=\{y+mean(y)\}/2\)
\(\eta=- \ln \{ 1/(\alpha\mu) +1 \}\)
WHILE ( abs( \(\Delta Dev\) ) > tolerance) {
\(W=\mu+\alpha \mu^2\)
\(Z=\{ \eta +(y-\mu)/W \}\)
\(\beta=(X^TWX)^{-1}X^TWZ\)
\(\eta = X\beta\)
\(\mu=1/\{ \alpha(e^{-\eta} -1 ) \}\)
OldDev=Dev
Dev = \(2\sum \{ y\ln(y/\mu) -(y+1/\alpha)\ln[(1+\alpha y)/(1+\alpha \mu)] \}\)
\(\Delta Dev\) =Dev - OldDev
}
\(\chi^2=\sum [ (y-\mu)^2/(\mu+\alpha \mu^2)]\)
图 18.3.1 NB-C IRLS
18.3.2. 参数 \(\alpha\) 的估计
(18.3.7) \[\frac{\partial \ell }{\partial \mu}
= \sum_{i=1}^N \frac{y_i - \mu_i}{\mu_i (1+\alpha \mu_i )}\]
(18.3.8) \[\frac{\partial \ell }{\partial \beta_j}
= \sum_{i=1}^N \frac{x_{ij} (y_i - \mu_i )}{1+\alpha \mu_i }\]
(18.3.9) \[\frac{\partial \ell }{\partial \alpha} = \sum_{i=1}^N
\left \{
\frac{1}{\alpha^2} \left [ \ln(1+\alpha \mu_i) +\frac{\alpha(y_i - \mu_i)}{1+\alpha \mu_i} \right ]
+ \psi \left ( y_i + \frac{1}{\alpha} \right )
- \psi \left ( \frac{1}{\alpha} \right )
\right \}\]
(18.3.10) \[\frac{\partial^2 \ell}{\partial \beta_j \beta_k} = \sum_{i=1}^N
\left [
-x_{ij}x_{ik} \frac{\mu_i(1+\alpha y_i)}{(1+\alpha \mu_i)^2}
\right ]\]
(18.3.11) \[\frac{\partial^2 \ell}{\partial \beta_j \partial \alpha } = \mathbb{E} \left [
- \sum_{i=1}^N
\frac{\mu_i(y_i - \mu_i)x_{ij}}{(1+\alpha \mu_i)^2}
\right ]\]
(18.3.12) \[ \begin{align}\begin{aligned}\frac{\partial^2 \ell}{\partial \alpha^2} = \sum_{i=1}^N
& \left \{
- \frac{1}{\alpha^3} \left [
\frac{\alpha(1+2\alpha \mu)(y_i-\mu_i) - \alpha \mu_i (1+\alpha \mu_i)}{(1+\alpha \mu_i)^2}
+ 2\ln(1+\alpha \mu_i)
\right ] \right.\\& \left. + \psi' \left ( y_i + \frac{1}{\alpha} \right )
- \psi' \left ( \frac{1}{\alpha} \right )
\right \}\end{aligned}\end{align} \]
18.4. 负二项式模型扩展
18.4.1. 对数连接函数采用对数连接的负二项式模型简称为 NB-2 \(\alpha=0\) 的
NB-2 NB-2 NB-C
把 NB-C NB2
连接函数: \(\eta=\ln(\mu)\)
响应函数: \(\mu=exp(\eta)\)
NB2
(18.4.1) \[f(y;\alpha,\mu)
= \exp \left \{
y \ln ( \mu )- \frac{1}{\alpha} \ln (1+\alpha \mu) + \ln \frac{\Gamma(y+1/\alpha) }{\Gamma(y+1) \Gamma(1/\alpha) }
\right \}\]
NB2
(18.4.2) \[D = 2\sum_{i=1}^N \left \{
y_i \ln \left ( \frac{y_i}{ \hat{\mu}_i} \right )
- \frac{1}{\alpha} \ln \left ( \frac{1+\alpha y_i}{1+\alpha \hat{\mu}_i} \right )
\right \}\]
NB2 IRLS NB-C NB2
(18.4.3) \[ \begin{align}\begin{aligned}\text{连接函数} \quad &\eta = g(\mu) = \ln (\mu)\\\text{连接函数一阶导} \quad &g'(\mu) = 1/\mu\\\text{连接函数二阶导} \quad &g''(\mu) = -1/\mu^2\\\text{方差} \quad &V(\mu) = a(\phi)\nu(\mu) = \mu+\alpha \mu^2\\\text{方差一阶导} \quad &V'(\mu) = 1+ 2\alpha \mu\\\text{方差的平方} \quad &V^2(\mu) = ( \mu+\alpha \mu^2)^2\end{aligned}\end{align} \]
IRLS \(W\) 和工作响应 \(Z\)
分别为
(18.4.4) \[ \begin{align}\begin{aligned}W &= \text{diag} \left \{ \frac{ 1}{ V(\hat{\mu}) ( g' )^2}
\right \}_{(N\times N)}\\&= \text{diag} \left \{
\frac{\mu}{1+\alpha \mu}
\right \}_{(N\times N)}\end{aligned}\end{align} \]
(18.4.5) \[ \begin{align}\begin{aligned}Z &= \left \{ (y- \hat{\mu}) g' + \eta
\right \}_{(N\times 1 )}\\ &= \left \{ \frac{(y- \hat{\mu})}{\hat{\mu}} + \eta
\right \}_{(N\times 1 )}\end{aligned}\end{align} \]
在传统的GLM算法中,参数估计算法IRLS使用的是期望信息矩阵 EIM NB-C EIM OIM NB-2 EIM OIM NB-2 OIM
备注
回顾一下,GLM OIM IRLS EIM OIM EIM OIM EIM EIM GLM OIM EIM IRLS
NB-2 \(\mu\)
,而 NB-2 \(\mu+\alpha \mu^2\)
,NB-2 \(\alpha \mu^2\)
,就是这多出来的一项使得 NB-2 \(\alpha\) 调节方差和期望的大小关系,
可以拟合泊松过度分散的数据,
因此 NB-2
18.4.2. 参数 \(\alpha\) 的估计辅助参数 \(\alpha\) 和分散参数 \(\phi\)
是不同的。分散参数 \(\phi\) 不影响协变量参数 \(\beta\)
的估计过程,因此可以在 IRLS \(\alpha\) 是会影响协变量参数 \(\beta\) 的估计过程的,
所以 \(\alpha\) 的估计是不同于 \(\phi\) 的。
负二项式模型中 \(\alpha\) 参数的确定一般有两种方法,一种是在 IRLS \(\alpha\) 的值,然后把它当成一个常量代入 IRLS GLM IRLS
如果需要模型自行估计 \(\alpha\)
,就需要修改 IRLS IRLS \(\alpha\) 的估计的过程。
在 IRLS \(\alpha\) 的估计过程,
\(\alpha\) 和 \(\beta\) 交替估计。
在一个迭代步骤中,先假设 \(\alpha\) 是已知的,执行 \(\beta\) 的估计过程,
然后再利用 \(\beta\) 的估计值,估计 \(\alpha\) 的值。
在 \(\beta\) 已知的情况下,可以利用皮尔逊分散统计量来估计 \(\alpha\)
。理论上,负二项式模型的分散统计量值为 \(1\)
,可以利用这个
(18.4.6) \[\hat{\phi}=\frac{\chi^2}{N-p}
= \sum \frac{(y_i-\mu_i)^2}{(N-p)(\mu_i - \alpha \mu^2_i)}
= 1\]
18.4.3. 几何模型当 \(\alpha=1\) 是,负二项式分布就变成了几何分布,
几何分布是负二项式分布的一个特例。
分别把 NB-C NB-2 \(\alpha\) 设置为 \(1\) 就得到了
标准连接和对数连接的几何分布。
标准连接的 NB-C 公式(18.2.7)
转换成几何分布的概率质量函数为
(18.4.7) \[f(y;\mu)
= \exp \left \{
y \ln \left (\frac{\mu}{1+\mu} \right )- \ln (1+\mu)
\right \}\]
对数连接的 NB-2 公式(18.4.7)
转换成几何分布的概率质量函数为
(18.4.8) \[f(y;\mu)
= \exp \left \{
y \ln ( \mu )- \ln (1+\mu)
\right \}\]
相比于负二项式分布,几何分布的概率质量函数没有了 Gamma
图 18.4.1 几何分布和指数分布近乎是一致的,
几何分布的期望是 \(\mu\)
,方差是 \(\mu+\mu^2\)
,各个关键组件为
(18.4.9) \[ \begin{align}\begin{aligned}\text{自然参数} & \quad \theta = \ln \left (\frac{ \mu}{1+ \mu} \right )\\
\text{累积分布函数} & \quad b(\theta) = \ln (1+\mu)\\\text{期望} & \quad b'(\theta) = \mu\\\text{方差函数} & \quad \nu(\mu) = b''(\theta) = \mu + \mu^2\\\text{分散函数} & \quad a(\phi) = 1\\\text{方差} & \quad V(Y) = a(\phi)\nu(\mu) = \mu + \mu^2 = \mu(1+\mu)\\\text{标准连接函数} & \quad g(\mu) = \ln \left (\frac{ \mu}{1+ \mu} \right )\\\text{标准连接函数一阶导} & \quad g'(\mu) = \frac{1}{\mu+ \mu^2}\end{aligned}\end{align} \]
标准连接的对数似然函数为
(18.4.10) \[ \begin{align}\begin{aligned}\ell(\mu;y)
&= \sum_{i=1}^N \left \{
y_i \ln \left (\frac{\mu_i}{1+\mu_i} \right )- \ln (1+\mu_i)
\right \}\\&=\sum_{i=1}^N \left \{
y_i \ln (\mu_i) - (1+y_i) \ln (1+\mu_i)
\right \}\end{aligned}\end{align} \]
标准连接的偏差统计量为
(18.4.11) \[\mathcal{D} =2\sum_{i=1}^N \left \{
y_i \ln \left (\frac{y_i}{\mu_i} \right )
-(1+y_i) \ln \left ( \frac{1+y_i}{1+\mu_i} \right )
\right \}\]
几何模型是一个单参数模型,因此可以直接应用 IRLS
18.4.4. 广义负二项式模型负二项式模型的方差函数为 \(\mu+\alpha \mu^2\)
,其中有一个 \(\mu\) 的二次项,
如果把二次项改成一次就变成了一个线性参数化方程,
我们把方差函数为 \(\mu+ \alpha \mu\) 的模型称为
线性负二项式模型,简称为 NB-1 \(\mu\)
,而这些扩展模型都是在泊松方差的基础上乘上一个因子,
不同的乘数因子形成了不同的泊松扩展模型。
NB-1 NB-2
NB-1 \(\mu+\alpha \mu\)
,NB-2 \(\mu+\alpha \mu^2\)
,二者的差别在于 \(\mu\) 的幂次不一样,
按照这个规律是不是可以有更高幂次的模型?
更进一步,是不是可以把幂次也参数化?
比如用参数 \(Q\)
参数化方差函数的最高幂次,
则方差函数变为
(18.4.12) \[V = \mu +\alpha \mu^Q\]
其中 \(Q\) 是一个待估计的的未知参数。
把方差函数的幂次参数化,相当于对负二项式模型的方差函数进行了一般化扩展,
因此我们称之为广义负二项式模型(generalized negative binomial),
一般简称为 NB-P
NB-P \(\mu\) ,辅助参数 \(\alpha\)
,以及参数 \(Q\)
,显然已经不再属于 GLM GLM IRLS