14. 泊松模型

前文我们讨论了离散数据模型中的二项式模型，二项式分布描述的是二值离散变量。 在离散数据中还有另一种数据形式，计数数据。 计数是对某一事件的简单计数，其取值是 \(0,1,2,...\) 等大于等于0的整数， 通常用于描述单位时间内某个事件的发生次数。 在指数族中，用于表示计数变量的概率分布是泊松分布(Poisson distribution)， 计数变量也被称为泊松变量， 该模型以Poisson（1837）提出的研究命名。

泊松分布和二项式分布是存在关联的，泊松分布可以看做是二项分布的极限情况， 二项式分布表示进行N次伯努利实验成功的次数，而泊松分布表示单位时间或者空间内事件发生的次数， 二者很相似，泊松分布就是二项式分布中N趋近于无穷时的情况。 本章我们先讨论如何从二项式分布推导出泊松分布，然后再讨论GLM家族中泊松模型的特性。

14.1. 泊松(Poisson)分布

泊松(Poisson)分布的直观理解是，在一个单位时间或者空间间隔内，随机事件发生次数的概率。 比如：

• 每个小时出生的婴儿数量

• 每分钟人类心脏的跳动次数

• 空气中每立方米中氧气分子的数量

• 高速公路上每公里汽车的数量

泊松模型是最基本的计数模型，本章我们重点讨论泊松模型，再后续的章节中再讨论其它的计数模型。

14.1.1. 推导过程

泊松分布实际上是二项分布的试验(trials)次数 \(N\) 趋近于无穷时的场景，我们用一个例子说明。 假设一个交通观察员需要对某个路口的车流量进行建模，然后用模型预测未来一个小时内从这个路口通过的车次。 为了简化问题，我们假设路口的交通量不存在高峰期低峰期，即交通量不会随着时间的变化而变化， 并且每个时间片段内通过的车辆是互不影响的，即前一小时内车辆通过与否不影响下一个小时车辆。 观察员首先根据这个路口历史上车辆通过情况，计算出平均每小时通过车辆的数量为 \(\lambda\) 。我们把一个小时内从路口通过的车次数看做一个随机变量，用符号 \(X\) 表示， 那么 \(\lambda\) 就是变量 \(X\) 的数学期望。

(14.1.1)\[\mathbb{E}[X] = \lambda\]

我们把一辆车通过与否看做是一个伯努利变量，类似投硬币实验，1表示车辆通过，0表示车辆不通过。 把一个小时的时间区间均分成 \(N\) 个时间片段，比如每分钟作为一个片段，这时 \(N=60\) 。 每个时间片段有车辆通过就是一次成功的实验(类似于投硬币正面向上)， 没有车辆通过就是一次失败的实验(类似于投硬币反面向上)， 这样就把一小时内车辆通过问题转化成一个二项分布问题， 在 \(N\) 次实验中有k次成功(车辆通过)概率分布函数可以写成：

(14.1.2)\[p(X=k) = \binom{N}{k} p^k \left ( 1-p \right )^{N-k}\]

其中 \(p\) 是一次实验的成功概率，我们已经通过历史数据知道平均每小时( \(N\) 次实验)中通过的车次数为 \(\lambda\) ，意味着n次实验中有 \(\lambda\) 次成功， 单次实验成功的概率(平均一分钟内通过车辆数)为：

(14.1.3)\[p = \frac{\lambda}{N}\]

但是我们并不能保证每分钟只有一辆车通过，我们需要保证一个时间片段内只有一辆车通过(一次实验) 以上的二项分布的假设才有意义。 理论上，我们只要把一小时的时间区间拆的足够小，比如拆成每秒，甚至是每毫秒为一个时间片段， 这样就能尽量保证每个时间片段内只会有一辆车通过。 \(N\) 越大时间片段就越小，极限情况，我们可以把一小时分割成每个车辆通过的”瞬间”。 换句话说，只要 \(N \to \infty\) 上述假设就是成立的，因此我们为 公式(14.1.2) 加上极限操作。

(14.1.4)\[p(X=k) = \lim_{N \to \infty} \binom{N}{k} p^k \left ( 1-p \right )^{N-k}\]

我们发现 公式(14.1.4) 就是二项分布的极限情况，表示的是路口未来一小时内通过的车辆数的概率分布， \(p(X=k)\) 表示在一小时内通过车辆数为 \(k\) 的概率。 \(\lambda\) 表示这个时间区间内通过车辆数的期望值， 至于这个时间区间是一小时还是两小时并不重要， 只要是一个固定的时间区间就行， 所以可以看成是单位时间区间内，或者 \(t\) 时间区间内。

公式(14.1.4) 带有极限操作，事实上可以通过一些变换去掉极限符号， 现在我们尝试对其进行一些变换。

(14.1.5)\[ \begin{align}\begin{aligned}p(X=k) &= \lim_{N \to \infty} \binom{N}{k} p^k \left ( 1-p \right )^{N-k}\\&= \lim_{N \to \infty} \frac{N!}{(N-k)!k!} \left (\frac{\lambda}{N} \right )^k \left ( 1-\frac{\lambda}{N} \right )^{N-k}\\&= \lim_{N \to \infty} \frac{N!}{(N-k)!k!} \frac{\lambda^k}{N^k} \left ( 1-\frac{\lambda}{N} \right )^N \left ( 1-\frac{\lambda}{N} \right )^{-k}\end{aligned}\end{align} \]

结合如下两个等式，

(14.1.6)\[\frac{N!}{(N-k)!} = \frac{N (N-1) \cdots 2\times 1}{(N-k)(N-k-1) \cdots 2\times 1} = \underbrace{N (N-1) \cdots (N-k+1)}_{\text{k个}}\]

(14.1.7)\[\lim_{x \to a} f(x)g(x) = \lim_{x \to a} f(x) \lim_{x \to a}g(x)\]

公式(14.1.5) 变成：

(14.1.8)\[ \begin{align}\begin{aligned}p(X=k) &= \lim_{N \to \infty} \frac{N (N-1) \cdots (N-k+1)}{N^k} \frac{\lambda^k}{k!} \left ( 1-\frac{\lambda}{N} \right )^N \left ( 1-\frac{\lambda}{N} \right )^{-k}\\&=\frac{\lambda^k}{k!} \lim_{N \to \infty} \left [ \frac{N (N-1) \cdots (N-k+1)}{N^k} \right ] \lim_{N \to \infty} \left [ \left ( 1-\frac{\lambda}{N} \right )^N \right ] \lim_{N \to \infty}\left [ \left ( 1-\frac{\lambda}{N} \right )^{-k}\right ]\end{aligned}\end{align} \]

其中各个极限都可以有近似表示。

(14.1.9)\[ \begin{align}\begin{aligned}\lim_{N \to \infty} \frac{N (N-1) \cdots (N-k+1)}{N^k} = 1\\\lim_{N \to \infty} \left ( 1-\frac{\lambda}{N} \right )^N = \lim_{N \to \infty} \left ( 1+\frac{-\lambda}{N} \right )^N = e^{-\lambda}\\\lim_{N \to \infty}\left [ \left ( 1-\frac{\lambda}{N} \right )^{-k}\right ] = 1\end{aligned}\end{align} \]

(14.1.10)\[p(X=k|N) = \frac{\lambda^k}{k!} \times 1 \times e^{-\lambda} \times 1 =\frac{\lambda^k}{k!} e^{-\lambda}\]

上式就表示在单位(固定)时间区间内，随机事件发生k次的概率，这就是泊松分布。 上式稍微整理下，就得到泊松分布的概率质量函数。

(14.1.11)\[p(x) = \frac{\lambda^x}{x!} e^{-\lambda}\]

其中变量 \(x\) 表示在单位时间内事件发生的次数，显然 \(x\) 是一个离散变量， 因此泊松分布是一个离散变量分布。 \(\lambda\) 是变量 \(x\) 的期望值，表示在单位时间内事件发生的平均次数， 因此通常也可以用 \(\mu\) 代替 \(\lambda\) 。

(14.1.12)\[p(x) = \frac{\mu^x}{x!} e^{-\mu}\]

二项式分布 \(Binomial(k,n)\) 表示进行 \(n\) 实验成功 \(k\) 次的概率， 需要知道 \(n\) 的值才行，并且没有时间区间的概念。 而泊松分布 \(Poisson(\lambda)\) 表示单位时间内事件发生 \(x\) 次的概率， 其用单位时间的概念替代了 \(n\) 的作用，并且这个单位时间具体多长并不重要，只是把整体时间分成相同长度的小片段。

注意，在泊松分布中，各个时间区间之间是相互独立的 ，互不影响， 也就是不会因为当前时间区间内有车辆通过，而导致下一个时间区间内通过的车辆受到影响。 泊松分布的应用并不是仅限于固定的时间区间，理论上只要是固定的区间(fixed interval)即可， 比如固定大小的时间、长度、空间、面积、体积等等。

14.1.2. 泊松分布的特性

通过泊松分布的概率质量函数 公式(14.1.12) ，可以看到泊松分布是一个单参数的分布， 其唯一的参数就是分布的期望值 \(\mu\) 。 理论上，泊松变量 \(X\) 可以取0值， 但泊松分布的期望值 \(\mu\) 一定是大于0的， 现在我们看下不同的 \(\mu\) 值下分布的差异。

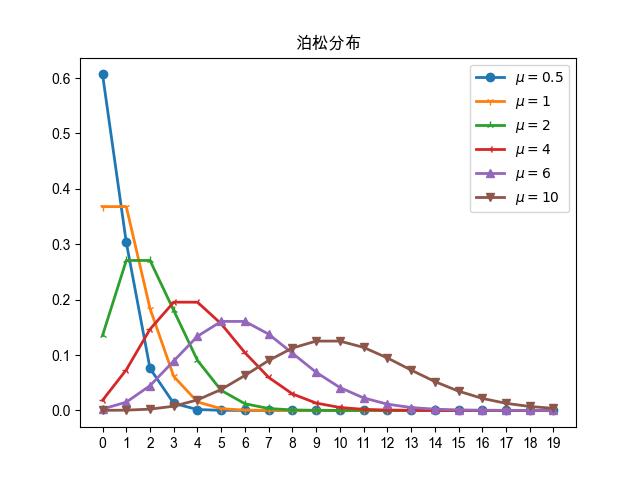
图 14.1.1 不同均值参数下泊松分布的概率质量函数

图 14.1.1 是不同的 \(\mu\) 下泊松分布的概率分布曲线。 从中可以看出当 \(\mu\) 比较小时，图形是偏态的， 随着 \(\mu\) 的增大，图形逐渐接近正态分布。

14.1.2.1. 分布的矩

14.2. 泊松回归模型

泊松分布的概率分布函数通常写成：

(14.2.1)\[f(y;\mu) = \frac{e^{-\mu} \mu^{y}}{y!}\]

其中阶乘部分可以用 \(\Gamma(y+1)\) 函数代替。

(14.2.2)\[f(y;\mu) = \frac{e^{-\mu} \mu^{y}}{\Gamma(y+1)}\]

现在转化成指数族的形式：

(14.2.3)\[f(y;\mu)=\exp \{ y\ln(\mu) -\mu- \ln \Gamma(y+1) \}\]

泊松分布的规范连接函数和累积函数为：

(14.2.4)\[ \begin{align}\begin{aligned}g(\mu) &= \theta=\ln(\mu)\\b(\theta) &= \mu\\a(\phi) &= 1\end{aligned}\end{align} \]

泊松分布的规范连接函数是对数(log)函数， 因此响应(反链接)函数就是指数函数， \(\mu=\exp(\eta)\) 。连接函数和响应函数的导数分别为：

(14.2.5)\[ \begin{align}\begin{aligned}g'(\mu) &= \frac{1}{\mu}\\ r'(\eta) &= \exp(\eta)\end{aligned}\end{align} \]

对 \(b(\theta)\) 求导得到其均值和方差函数。

(14.2.6)\[ \begin{align}\begin{aligned}b'(\theta) &= \frac{\partial b}{\partial \mu} \frac{\partial \mu}{\partial \theta}\\&= (1)(\mu)\\&= \mu\\ b''(\theta) &= \frac{\partial^2 b}{\partial \mu^2} \left( \frac{\partial \mu}{\partial \theta} \right )^2 +\frac{\partial b}{\partial \mu} \frac{\partial^2 \mu }{\partial \theta^2}\\&= (0)(1)^2+(\mu)(1)\\&= \mu\end{aligned}\end{align} \]

泊松分布的方差为 \(V(y)=a(\phi)b''(\theta)=\mu\) ，我们发现，泊松分布的方差和均值是相同的， 牢记泊松分布的这个特点，后续我们会详细讨论这个特点带来的一些影响。 因为泊松分布的方差和均值相同，所以泊松分布的变异系数是 \(c_{\nu} = \frac{\sqrt{\mu}}{\mu} =1/\sqrt{\mu}\) 。

备注

变异系数(Coefficient of Variation)，又称“离散系数”、“变差系数”，是概率分布离散程度的一个归一化量度，其定义为标准差与平均值之比。 当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响， 而变异系数可以做到这一点，它是原始数据标准差与原始数据平均数的比。变异系数没有量纲，这样就可以进行客观比较了。 事实上，可以认为变异系数和极差、标准差和方差一样，都是反映数据离散程度的绝对值。其数据大小不仅受变量值离散程度的影响，而且还受变量值平均水平大小的影响。

最后总结一下泊松模型的关键部分。

(14.2.7)\[ \begin{align}\begin{aligned}\text{标准连接函数：} & \eta= g(\mu) = \ln(\mu)\\\text{反链接(响应)函数：} & \mu=r(\eta) = \exp(\eta)\\\text{方差函数：} & \nu= \mu\\\text{分散函数：} & a(\phi) = 1\\\text{连接函数导数：} & g'= \frac{1}{\mu}\end{aligned}\end{align} \]

14.3. 参数估计

GLM中泊松模型的参数估计，同样可以应用IRLS算法解决， 按照前文讨论的IRLS算法的过程，我们只需要求出泊松模型对应的 \(W\) 矩阵和 \(Z\) 矩阵即可，先从泊松模型的对数似然函数开始。 泊松模型的对数似然函数可以直接写出。

(14.3.1)\[\ell(\hat{\mu};y) = \sum_{i=1}^N \{ y_i \ln(\hat{\mu}_i) -\hat{\mu}_i-\ln \Gamma(y_i+1) \}\]

根据 公式(8.1.12) ，泊松模型的得分统计量为

(14.3.2)\[ \begin{align}\begin{aligned}U_j = \frac{\partial \ell}{\partial \beta_j} &= \sum_{i=1}^N \frac{y_i-\hat{\mu}_i}{a(\phi) \nu(\hat{\mu}_i) g(\hat{\mu}_i)' } x_{ij}\\&= \sum_{i=1}^N (y_i-\hat{\mu}_i) x_{ij}\end{aligned}\end{align} \]

泊松模型的 \(W\) 和 \(Z\) 分别为

(14.3.3)\[ \begin{align}\begin{aligned}W_{ii} &= \frac{ 1}{ a(\phi) \nu(\hat{\mu}_i) ( g_i' )^2}\\&= \hat{\mu}_i\end{aligned}\end{align} \]

(14.3.4)\[ \begin{align}\begin{aligned}Z_i &= (y_i- \hat{\mu}_i) g_i' + \eta_i\\ &= \frac{(y_i- \hat{\mu}_i)}{ \hat{\mu}_i} + \eta_i\end{aligned}\end{align} \]

14.4. 拟合统计量

我们知道，在 GLM 中评估模型优劣的方法一般有三种，拟合优度统计量(goodness-of-fit statistic)、 残差统计量(residual statistic)、以及AIC、BIC等信息量准则。 在拟合优度统计量中，最常用的就是偏差统计量，泊松模型的偏差统计量为：

(14.4.1)\[ \begin{align}\begin{aligned}D &=2 \{ \ell(y;y) - \ell(\hat{\mu};y) \}\\&= 2\sum_{i=1}^n \{ y_i \ln(y_i) -y_i - y_i \ln(\hat{\mu}_i) +\hat{\mu}_i \}\\&= 2\sum_{i=1}^n \left \{ y_i \ln \left ( \frac{y_i}{\hat{\mu}_i} \right ) - (y_i - \hat{\mu}_i) \right \}\end{aligned}\end{align} \]

上述偏差统计量的计算公式有个问题，就是当响应数据 \(y_i=0\) 时， \(\ln ( y_i/\hat{\mu}_i )\) 是没有意义的，所以需要单独处理0值的数据。 当 \(y_i=0\) 时，其预测模型的对数似然函数简化为：

(14.4.2)\[\ell_i(\hat{\mu}_i;0) = -\hat{\mu}_i\]

此时，饱和模型的对数似然函数为：

(14.4.3)\[\ell_i(0;0) = 0\]

因此，对于响应数据 \(y_i=0\) 的样本，其偏差为：

(14.4.4)\[D_i(y_i=0) = 2\hat{\mu}_i\]

泊松模型的皮尔逊卡方统计量为

(14.4.5)\[ \begin{align}\begin{aligned}\chi^2 &= \sum_{i=1}^N \frac{ (y_i-\hat{\mu}_i)^2}{\nu(\hat{\mu}_i)}\\&= \sum_{i=1}^N \frac{ (y_i-\hat{\mu}_i)^2}{\hat{\mu}}\end{aligned}\end{align} \]

14.5. 频率模型

单位时间内发生的次数就是频次或者频率，因此泊松分布也可以看做是对频率数据进行建模， 通常泊松分布可以引入一个表示时间或者空间的常量系数 \(t\) 。

(14.5.1)\[f(y;\mu) = \frac{e^{-t\mu} (t\mu)^{y}}{y!}\]

常数系数 \(t\) 表示时间长度或者空间大小，\(\mu\) 表示频率参数， \(t\mu\) 就表示在长度为 \(t\) 的时间或者空间窗口内事件发生的次数的期望值。 当 \(t=1\) 是就退化成泊松分布的标准形式。

14.6. 泊松模型的局限性